Thursday, March 31, 2016
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2015$-$2016 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
Bài 1. (3 điểm) Thực hiện phép tính:
a) $\dfrac{{ - 1}}{4} + \dfrac{7}{3} - \dfrac{5}{2}$
b) $\dfrac{{ - 23}}{5}.\dfrac{3}{4} + \dfrac{3}{4}.\dfrac{{13}}{5}$c) $\dfrac{{ - 17}}{{19}} + \dfrac{{15}}{{23}} + \dfrac{{ - 2}}{{19}} + \dfrac{8}{{23}}$
d) $\left( { - 3,5} \right) + 1\dfrac{1}{2}:\left( {\dfrac{2}{3} - \dfrac{5}{6}} \right)$
Bài 2. (2,5 điểm) Tìm x, biết:
a) $x + \dfrac{3}{4} = \dfrac{{ - 1}}{6}$
b) $\dfrac{1}{4} - \dfrac{3}{4}x = \dfrac{7}{{16}}$
c) $\left( {x + \dfrac{{11}}{2}} \right).\dfrac{7}{3} - 3 = \dfrac{1}{2}$
b) $\dfrac{1}{4} - \dfrac{3}{4}x = \dfrac{7}{{16}}$
c) $\left( {x + \dfrac{{11}}{2}} \right).\dfrac{7}{3} - 3 = \dfrac{1}{2}$
Bài 3. (1 điểm) Thẻ nhớ di động (USB) là một thiết bị nhỏ dùng để lưu trữ dữ liệu máy tính. Nam có một chiếc thẻ nhớ dung lượng 1 GB (= 1000 MB), Nam dùng $\dfrac{1}{4}$ dung lượng thẻ nhớ để lưu trữ nhạc và 50% dung lượng thẻ nhớ để lưu trữ hình ảnh.
a) Em hãy tính dung lượng của thẻ nhớ theo đơn vị MB mà Nam dùng để lưu trữ nhạc.
b) Nam muốn chuyển một đoạn phim có dung lượng 350 MB vào chiếc thẻ nhớ của bạn ấy. Theo em thẻ nhớ của bạn Nam có còn đủ dung lượng để lưu trữ đoạn phim không? Vì sao?
Bài 4. (3 điểm) Trên cùng một nửa mặt phẳng có bờ chứa tia Ox, vẽ hai tia Oy và Oz sao cho $\widehat {xOy} = {150^0}$ và $\widehat {xOz} = {75^0}$.
a) Trong ba tia Ox, Oy, Oz thì tia nào nằm giữa hai tia còn lại? Vì sao?
b) Tính số đo $\widehat {yOz}$.
c) Tia Oz có là tia phân giác của $\widehat {xOy}$ không? Vì sao?
d) Vẽ tia Om là tia đối của tia Oy, tia Ot là tia phân giác của $\widehat {mOx}$. Tính số đo $\widehat {zOt}$.
Bài 5. (0,5 điểm) Tính hợp lý:
$M = \dfrac{2}{3} + \dfrac{9}{{10}} - \dfrac{{11}}{{15}} + \dfrac{{13}}{{21}} - \dfrac{{15}}{{28}} + \dfrac{{17}}{{36}} - \dfrac{{19}}{{45}} + \dfrac{{21}}{{55}} - \dfrac{{23}}{{66}}$
Tuesday, March 29, 2016
I. RATIO OF TWO NUMBERS
_ The quotient in the division of number $a$ by number $b$ ($b$ $ \ne $ 0) is called the ratio of $a$ to $b$.
_ The ratio of $a$ to $b$ is denoted by $a$ : $b$ or $\dfrac{a}{b}$.
Example: 1.7 : 3.12; $\dfrac{1}{5}:\dfrac{3}{4}$; $ - 3\dfrac{1}{4}:5$; ... are ratios.
* Note: When we say ratio $\dfrac{a}{b}$, then $a$ and $b$ can be integers, fractions, mixed numbers, …, on the other hand, for fraction $\dfrac{a}{b}$, both $a$ and $b$ must be integers.
_ The ratio of $a$ to $b$ is denoted by $a$ : $b$ or $\dfrac{a}{b}$.
Example: 1.7 : 3.12; $\dfrac{1}{5}:\dfrac{3}{4}$; $ - 3\dfrac{1}{4}:5$; ... are ratios.
* Note: When we say ratio $\dfrac{a}{b}$, then $a$ and $b$ can be integers, fractions, mixed numbers, …, on the other hand, for fraction $\dfrac{a}{b}$, both $a$ and $b$ must be integers.
II. PERCENTAGE
Rule: To find the percentage of $a$ to $b$, we compute $\dfrac{{a.100}}{b}\% $.
Example: Find the percentage of:
a) $5$ và $8$
The percentage of $5$ to $8$ is:
$\dfrac{5}{8} = \dfrac{{5 \times 100}}{8}\% = 62.5\% $
b) 25kg và $\dfrac{3}{{10}}$quintal
$\dfrac{3}{{10}}$quintal = $\dfrac{3}{{10}}$ $\times$ 100kg = 30kg
The percentage of 25kg to $\dfrac{3}{{10}}$quintal is:
$\dfrac{{25}}{{30}} = \dfrac{5}{6} = \dfrac{{5 \times 100}}{6}\% = 83.3\% $
III. SCALE
Scale $T$ of a drawing (or a map) is the
ratio of distance $a$ between two points on the drawing (or the map) to distance $b$ between two points in corresponding reality: $T = \dfrac{a}{b}$ (a, b have the
same unit of measurement).
Example: If the
distance $a$ on a map is 1cm, the actual distance $b$ is 1km, the map scale $T$ is 1
: 100000.
Monday, March 28, 2016
I. TỈ SỐ CỦA HAI SỐ
_ Thương trong phép chia số $a$ cho số $b$ ($b \ne $ 0) gọi là tỉ số của $a$ và $b$.
_ Tỉ số của $a$ và $b$ kí hiệu là $a : b$ hoặc $\dfrac{a}{b}$.
Ví dụ: $1,7 : 3,12$; $\dfrac{1}{5}:\dfrac{3}{4}$; $ - 3\dfrac{1}{4}:5$; ... là những tỉ số.
* Lưu ý: Khi ta nói tỉ số $\dfrac{a}{b}$ thì $a$ và $b$ có thể là các số nguyên, phân số, hỗn số, …, còn khi nói phân số $\dfrac{a}{b}$ thì cả $a$ và $b$ phải là các số nguyên.
II. TỈ SỐ PHẦN TRĂM
Qui tắc: Muốn tìm tỉ số phần trăm của $a$ và $b$, ta tính $\dfrac{{a.100}}{b}\% $.
Ví dụ: Tìm tỉ số phần trăm của:
a) $5$ và $8$
Tỉ số phần trăm của $5$ và $8$ là: $\dfrac{5}{8} = \dfrac{{5.100}}{8}\% = 62,5\% $
b) 25kg và $\dfrac{3}{{10}}$ tạ
$\dfrac{3}{{10}}$ tạ = $\dfrac{3}{{10}}$.$100$kg = $30$kg
Tỉ số phần trăm của 25kg và $\dfrac{3}{{10}}$ tạ là: $\dfrac{{25}}{{30}} = \dfrac{5}{6} = \dfrac{{5.100}}{6}\% \approx 83,3\% $
III. TỈ LỆ XÍCH
Tỉ lệ xích $T$ của một bản vẽ (hoặc một bản
đồ) là tỉ số khoảng cách $a$ giữa hai điểm trên bản vẽ (hoặc bản đồ) và khoảng
cách $b$ giữa hai điểm tương ứng trên thực tế: $T = \dfrac{a}{b}$ (a, b có cùng đơn vị
đo)
Ví dụ: Nếu
khoảng cách $a$ trên bản đồ là 1cm, khoảng cách $b$ trên thực tế là 1km thì tỉ lệ
xích $T$ của bản đồ là 1 : 100000.
Sunday, March 27, 2016
Saturday, March 26, 2016
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2014$-$2015 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
a) $\dfrac{1}{6} + \dfrac{7}{3} - \dfrac{1}{2}$Bài 1. (3 điểm) Thực hiện phép tính:
b) $\dfrac{{ - 3}}{8}.\dfrac{2}{5} + \dfrac{{ - 3}}{8}.\dfrac{{14}}{5}$
c) $\left| { - 1\dfrac{5}{8}} \right| + 1,25:\left( {1 - \dfrac{9}{4}} \right)$
d) $\left( {\dfrac{1}{4} + \dfrac{{11}}{9}} \right):\dfrac{{34}}{5} + \left( {\dfrac{{ - 2}}{9} + \dfrac{{29}}{4}} \right):\dfrac{{34}}{5}$
Bài 2. (2,5 điểm) Tìm x, biết:
a) $x + \dfrac{7}{12} = \dfrac{-5}{6}$
b) $\left( {\dfrac{2}{9} - x} \right):\dfrac{5}{6} = \dfrac{{ - 4}}{3}$
c) $\dfrac{{ - 1}}{2} = \dfrac{{x - 1}}{6}$
b) $\left( {\dfrac{2}{9} - x} \right):\dfrac{5}{6} = \dfrac{{ - 4}}{3}$
c) $\dfrac{{ - 1}}{2} = \dfrac{{x - 1}}{6}$
Bài 3. (1 điểm)
Một khu đất hình
chữ nhật có chiều dài 18km và chiều rộng bằng $\dfrac{5}{9}$ của chiều dài. Tính
chiều rộng và diện tích của khu đất.
Bài 4. (3 điểm) Trên cùng một nửa mặt phẳng có bờ chứa
tia Ox, vẽ hai tia Oy và Om sao cho $\widehat {xOy} = {50^0}$ và $\widehat {xOm} = {100^0}$.
a) Trong ba tia Ox, Oy, Om thì tia
nào nằm giữa hai tia còn lại? Vì sao?
b) So sánh $\widehat {xOy}$ và $\widehat {yOm}$.
c) Tia Oy có phải là tia phân giác của $\widehat {xOm}$ không? Vì sao?
d) Vẽ tia Oh là tia đối của tia Ox.
Tính $\widehat {yOh}$.
Bài 5. (0,5 điểm) Tính hợp lý:
$M = \dfrac{3}{2} - \dfrac{5}{6} + \dfrac{7}{{12}} - \dfrac{9}{{20}} + \dfrac{{11}}{{30}} - \dfrac{{13}}{{42}} + \dfrac{{15}}{{56}} - \dfrac{{17}}{{72}}$Friday, March 25, 2016
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2013$-$2014 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
a) $\dfrac{{ - 3}}{4} + \dfrac{7}{3} - \dfrac{1}{2}$Bài 1. (3 điểm) Thực hiện phép tính:
b) $\dfrac{{ - 3}}{4}.\dfrac{7}{6} + \dfrac{5}{6}.\dfrac{{ - 3}}{4}$
c) $1\dfrac{1}{2}:\left( {\dfrac{2}{3} - \dfrac{1}{6}} \right) + 1,5$
d) $\dfrac{3}{4}:{\left( {\dfrac{1}{2}.\dfrac{{ - 6}}{5} + \dfrac{{13}}{5}} \right)^2}$
Bài 2. (2,5 điểm) Tìm x, biết:
a) $x + \dfrac{7}{9} = \dfrac{5}{6}$
b) $\dfrac{2}{5} + \dfrac{3}{5}x = \dfrac{{ - 7}}{{10}}$
c) $\left( {x - \dfrac{1}{2}} \right).\dfrac{9}{2} - 4 = \dfrac{1}{2}$
b) $\dfrac{2}{5} + \dfrac{3}{5}x = \dfrac{{ - 7}}{{10}}$
c) $\left( {x - \dfrac{1}{2}} \right).\dfrac{9}{2} - 4 = \dfrac{1}{2}$
Bài 3. (1 điểm)
Tính diện tích và chu vi một khu đất hình chữ nhật
có chiều dài là $\dfrac{1}{4}$ km và chiều rộng là $\dfrac{1}{8}$ km.
Bài 4. (3 điểm) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy và Oz sao cho $\widehat {xOy} = {50^0}$, $\widehat {xOz} = {100^0}$.
a) Trong ba tia Ox, Oy, Ox thì tia nào nằm giữa hai tia còn lại? Vì sao?
b) Tính số đo $\widehat {yOz}$.
c) Tia Oy có là tia phân giác của $\widehat {xOz}$ không? Vì sao?
d) Vẽ tia Om là tia đối của tia Oy, tia Ot là tia phân giác của $\widehat {mOz}$. Tính số đo $\widehat {yOt}$.
Bài 5. (0,5 điểm) Tính hợp lý:
$M = \dfrac{1}{2} + \dfrac{5}{6} + \dfrac{{11}}{{12}} + \dfrac{{19}}{{20}} + \dfrac{{29}}{{30}} + \dfrac{{41}}{{42}} + \dfrac{{55}}{{56}} + \dfrac{{71}}{{72}} + \dfrac{{89}}{{90}}$Thursday, March 24, 2016
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2011$-$2012 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
a) $\dfrac{5}{{12}} - \dfrac{1}{6} + \dfrac{7}{{12}}$Bài 1. (3 điểm) Thực hiện phép tính:
b) $\dfrac{1}{4}:\dfrac{3}{2} - 25\% $
c) $\dfrac{{ - 2}}{7}.\dfrac{3}{{11}} + \dfrac{{ - 2}}{7}.\dfrac{{19}}{{11}} + \dfrac{{11}}{7}$
d) $2\dfrac{2}{9} - 3\dfrac{1}{8} + 1\dfrac{7}{9}$
Bài 2. (2,5 điểm) Tìm x, biết:
a) $x - \dfrac{7}{{10}} = \dfrac{{ - 1}}{5}$
b) $\dfrac{2}{3}x + \dfrac{1}{3} = \dfrac{5}{6}$
c) $\left( {x - \dfrac{3}{4}} \right):7 + \dfrac{5}{4} = 1$
b) $\dfrac{2}{3}x + \dfrac{1}{3} = \dfrac{5}{6}$
c) $\left( {x - \dfrac{3}{4}} \right):7 + \dfrac{5}{4} = 1$
Bài 3. (1 điểm)
a) So sánh: $\dfrac{7}{4}$ và $\dfrac{-3}{5}$
b) Người ta đóng 333 lít nước khoáng vào loại chai $\dfrac{1}{3}$ lít. Hỏi đóng được tất cả bao nhiêu chai?
b) Người ta đóng 333 lít nước khoáng vào loại chai $\dfrac{1}{3}$ lít. Hỏi đóng được tất cả bao nhiêu chai?
Bài 4. (3 điểm) Trên cùng một nửa mặt phẳng bờ chứa
tia OA, vẽ các tia OB, OC sao cho $\widehat {AOB} = {50^0}$, $\widehat {AOC} = {100^0}$.
a) Trong ba tia OA, OB, OC tia nào nằm
giữa hai tia còn lại? Vì sao?
b) Tính số đo $\widehat {BOC}$.
c) Chứng tỏ tia OB là tia phân giác
của $\widehat {AOC}$.
d) Vẽ tia OD là tia đối của tia OA,
Ox là tia phân giác của $\widehat {DOC}$. Tính số đo $\widehat {xOB}$.
Bài 5. (0,5 điểm) Tính hợp lý:
$A = \left( {\dfrac{1}{{2011}} + \dfrac{2}{{2010}} + \dfrac{3}{{2009}} + 4} \right):\left( {\dfrac{1}{{2009}} + \dfrac{1}{{2010}} + \dfrac{1}{{2011}} + \dfrac{1}{{2012}}} \right)$Tuesday, March 22, 2016
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2010$-$2011 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
a) $\dfrac{2}{3} - \dfrac{5}{6} + \dfrac{1}{2}$Bài 1. (3 điểm) Thực hiện phép tính:
b) $\left( {0,75 - \dfrac{1}{4}} \right):\dfrac{5}{8}$
c) $\dfrac{{ - 7}}{8}.\dfrac{1}{4} + \dfrac{3}{4}.\dfrac{{ - 7}}{8}$
d) $\dfrac{1}{5} + \dfrac{4}{5}.\dfrac{{ - 5}}{3} + \dfrac{2}{3}$
Bài 2. (2,5 điểm) Tìm x, biết:
a) $x - \dfrac{4}{3} = \dfrac{{ - 5}}{4}$
b) $\dfrac{1}{4} + \dfrac{5}{4}x = \dfrac{3}{8}$
c) $\left( {\dfrac{7}{2} - 3x} \right).\dfrac{8}{3} = \dfrac{4}{3}$
b) $\dfrac{1}{4} + \dfrac{5}{4}x = \dfrac{3}{8}$
c) $\left( {\dfrac{7}{2} - 3x} \right).\dfrac{8}{3} = \dfrac{4}{3}$
Bài 3. (2 điểm)
a) So sánh: $\dfrac{-3}{8}$ và $\dfrac{2}{-5}$
b) Tổng kết cuối năm, lớp 6B có 35 học sinh gồm 3
loại: giỏi, khá, trung bình. Trong đó, số học sinh giỏi bằng 40% số học sinh của
lớp, số học sinh khá bằng $\dfrac{9}{7}$ số học sinh giỏi. Tính
số học sinh trung bình của lớp 6B.
Bài 4. (2 điểm) Trên cùng một nửa
mặt phẳng bờ chứa tia Ox, vẽ hai tia Oy, Oz sao cho $\widehat {xOy} = {70^0}$, $\widehat {xOz} = {125^0}$.
a) Trong ba tia Ox, Oy, Oz tia nào nằm
giữa hai tia còn lại? Vì sao?
b) Tính số đo góc yOz.
c) Vẽ tia Ot là tia đối của tia Ox.
Tính số đo góc zOt.
d)
Tia Oz có là tia phân giác của góc tOy không? Vì sao?
Bài 5. (0,5 điểm) Thực hiện phép tính sau:
$A = \left( {1 + \dfrac{1}{{1.3}}} \right)\left( {1 + \dfrac{1}{{2.4}}} \right)\left( {1 + \dfrac{1}{{3.5}}} \right) \ldots \left( {1 + \dfrac{1}{{17.19}}} \right)\left( {1 + \dfrac{1}{{18.20}}} \right)$
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2009$-$2010 QUẬN 11 TPHCM
Bài 1. (2,5 điểm) Thực hiện phép tính:
$A = \dfrac{3}{4} - \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{2}{5}$Bài 1. (2,5 điểm) Thực hiện phép tính:
$B = 1\dfrac{1}{4}.\left( {\dfrac{2}{3} - \dfrac{2}{5}} \right)$
$C = \dfrac{{ - 4}}{5}:\dfrac{8}{{15}}$
Bài 2. (2,5 điểm) Tìm x, cho biết:
a) $x + \dfrac{7}{{10}} = \dfrac{2}{5}$
b) $\dfrac{2}{3}x - \dfrac{1}{4} = \dfrac{3}{5}$
c) $2x - 5 = x - 3$
b) $\dfrac{2}{3}x - \dfrac{1}{4} = \dfrac{3}{5}$
c) $2x - 5 = x - 3$
Bài 3. (2 điểm)
a) Sắp xếp theo thứ tự từ nhỏ đến lớn các phân số: $\dfrac{3}{4}$, $-\dfrac{4}{5}$, $\dfrac{5}{6}$, $-\dfrac{2}{3}$
b) Một lớp 6 có 40 học sinh. Cuối
năm học, số học sinh giỏi chiếm $\dfrac{1}{5}$ số học sinh của lớp,
số học sinh khá chiếm $\dfrac{5}{8}$ số học sinh của lớp,
còn lại là học sinh trung bình. Tìm số học sinh xếp loại trung bình của lớp.
Bài 4. (1 điểm) Tính giá trị biểu thức:
$C = \left( {1 - \dfrac{1}{2}} \right)\left( {1 - \dfrac{1}{3}} \right)\left( {1 - \dfrac{1}{4}} \right)\left( {1 - \dfrac{1}{5}} \right) \ldots \left( {1 - \dfrac{1}{{99}}} \right)\left( {1 - \dfrac{1}{{100}}} \right)$
$D = \dfrac{{{2^{18}}{3^{16}} - {2^{16}}{3^{15}}}}{{{2^{17}}{3^{17}} + {2^{16}}{3^{15}}}}$
Bài 5. (2 điểm) Cho điểm O trên
đường thẳng xy. Trên cùng nửa mặt phẳng bờ là đường thẳng xy, vẽ các tia Om, On
sao cho $\widehat {xOm} = {58^0}$, $\widehat {xOn} = {119^0}$.
a) Tính số đo $\widehat {mOn}$, $\widehat {nOy}$
b) Kẻ
tia Ot là tia đối của tia Om. Tính số đo $\widehat {tOy}$, $\widehat {tOn}$.
Monday, March 21, 2016
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2008$-$2009 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
$A = \dfrac{2}{3}.\left( {\dfrac{1}{2} + \dfrac{7}{4}} \right)$Bài 1. (3 điểm) Thực hiện phép tính:
$B = 6\dfrac{2}{5} - \left( {3\dfrac{1}{2} + 2\dfrac{2}{5}} \right)$
$C = \dfrac{{9.13 + 63}}{{9.19 - 36}}$
Bài 2. (2 điểm) Tìm x, cho biết:
a) $x - \dfrac{3}{{20}} = \dfrac{1}{4}$
b) $\dfrac{5}{6}x + \dfrac{3}{4} = \dfrac{1}{3}$
b) $\dfrac{5}{6}x + \dfrac{3}{4} = \dfrac{1}{3}$
Bài 3. (2 điểm)
a) So sánh hai phân số: $\dfrac{2}{3}$ và $\dfrac{5}{7}$
b) An có 24 viên bi, số bi của Hòa bằng $\dfrac{7}{8}$ số bi của An. Hỏi Hòa có bao nhiêu viên bi?
Bài 4. (1 điểm) Tính giá trị biểu thức:
$D = \dfrac{1}{6} + \dfrac{1}{{10}} + \dfrac{1}{{15}} + \dfrac{1}{{21}} + \dfrac{1}{{28}} + \dfrac{1}{{36}} + \dfrac{1}{{45}}$
Bài 5. (2 điểm) Trên cùng nửa mặt phẳng bờ chứa
tia Ox, vẽ hai tia Oy, Oz sao cho $\widehat {xOy} = {36^0}$, $\widehat {xOz} = {144^0}$.
a) Tính số đo $\widehat {yOz}$.
b) Kẻ tia Ot là tia đối của tia Oz.
Hỏi tia Ox có là tia phân giác của $\widehat {yOt}$ không? Vì sao?
Sunday, March 20, 2016
❄ QUADRATIC EQUATION IN ONE VARIABLE
The standard form
${a{x^2} + bx + c = 0}$
where x is unknown; a, b and c are real numbers with $a \ne 0$.
General quadratic equation
Calculate $\Delta = {b^2} - 4ac$
$\Delta < 0$ $ \Rightarrow $ the equation has no solution
$\Delta = 0$ $ \Rightarrow $ the equation has a double solution: ${x_{1,2}} = \dfrac{{ - b}}{{2a}}$
$\Delta > 0$ $ \Rightarrow $ the equation has two distinct solutions: ${x_{1,2}} = \dfrac{{ - b \pm \sqrt \Delta }}{{2a}}$
+ In the cases when the coefficient b is an even number
* In special cases:
If $b = 0$ or $c = 0$, we convert the quadratic equation in to the product equation.
$a + b + c = 0$ $ \Rightarrow $ ${x_1} = 1$, ${x_2} = \dfrac{c}{a}$
$a - b + c = 0$ $ \Rightarrow $ ${x_1} = -1$, ${x_2} = \dfrac{-c}{a}$
$a + b + c = 0$ $ \Rightarrow $ ${x_1} = 1$, ${x_2} = \dfrac{c}{a}$
$a - b + c = 0$ $ \Rightarrow $ ${x_1} = -1$, ${x_2} = \dfrac{-c}{a}$
Example. Solve the following equations:
1) ${x^2} + 4x = 0$
eqn $ \Leftrightarrow x\left( {x + 4} \right) = 0$
$ \Leftrightarrow x = 0\;or\;x + 4 = 0$
$ \Leftrightarrow x = 0\;or\;x = -4$
The equation has two solutions $x = 0,\;x = -4$.
2) ${x^2} - 9 = 0$
eqn $ \Leftrightarrow \left( {x - 3} \right)\left( {x + 3} \right) = 0$
$ \Leftrightarrow x - 3 = 0\;or\;x + 3 = 0$
$ \Leftrightarrow x = 3\;or\;x = -3$
The equation has two solutions $x = 3,\;x = -3$.
3) ${x^2} +1 = 0$
We have:
${x^2} \ge 0$ for all $x \in$ $\mathbb{R}$
$ \Rightarrow {x^2} + 1 \ge 1 > 0$
Therefore, the equation has no solution.
4) ${{x^2} - 5x + 6 = 0}$
1) ${x^2} + 4x = 0$
eqn $ \Leftrightarrow x\left( {x + 4} \right) = 0$
$ \Leftrightarrow x = 0\;or\;x + 4 = 0$
$ \Leftrightarrow x = 0\;or\;x = -4$
The equation has two solutions $x = 0,\;x = -4$.
2) ${x^2} - 9 = 0$
eqn $ \Leftrightarrow \left( {x - 3} \right)\left( {x + 3} \right) = 0$
$ \Leftrightarrow x - 3 = 0\;or\;x + 3 = 0$
$ \Leftrightarrow x = 3\;or\;x = -3$
The equation has two solutions $x = 3,\;x = -3$.
3) ${x^2} +1 = 0$
We have:
${x^2} \ge 0$ for all $x \in$ $\mathbb{R}$
$ \Rightarrow {x^2} + 1 \ge 1 > 0$
Therefore, the equation has no solution.
4) ${{x^2} - 5x + 6 = 0}$
$\left( {a = 1,\;b = - 5,\;c = 6} \right)$
$\Delta = {\left( { - 5} \right)^2} - 4.1.6 = 25 - 24 = 1 > 0$
The equation has two distinct solutions:
${x_1} = \dfrac{{ - \left( { - 5} \right) - \sqrt 1 }}{{2.1}} = 2$, ${x_2} = \dfrac{{ - \left( { - 5} \right) + \sqrt 1 }}{{2.1}} = 3$.
5) ${x^2} - \sqrt 5 x + \dfrac{5}{4} = 0$
$\left( {a = 1,\;b = - \sqrt 5 ,\;c = \dfrac{5}{4}} \right)$
$\Delta = {\left( { - \sqrt 5 } \right)^2} - 4.1.\dfrac{5}{4} = 5 - 5 = 0$
The equation has a double solution: $x = \dfrac{{ - \left( { - \sqrt 5 } \right)}}{{2.1}} = \dfrac{{\sqrt 5 }}{2}$.
6) ${2{x^2} + 3x + 2 = 0}$
$\left( {a = 2,\;b = 3,\;c = 2} \right)$
$\Delta = {3^2} - 4.2.2 = 9 - 16 = - 7 < 0$
The equation has no solution.
7) ${{x^2} - 3x + 2 = 0}$
$\left( {a = 1,\;b = -3,\;c = 2} \right)$
The equation of the form $a + b + c = 0$
$ \Rightarrow $ The equation has two solutions ${x_1} = 1$, ${x_2} = \dfrac{2}{1} = 2$
8) ${{x^2} - 4x - 5 = 0}$
$\left( {a = 1,\;b = -4,\;c = -5} \right)$
The equation of the form $a - b + c = 0$
$ \Rightarrow $ The equation has two solutions ${x_1} = -1$, ${x_2} = \dfrac{{ - \left( { - 5} \right)}}{1} = 5$
The equation has no solution.
7) ${{x^2} - 3x + 2 = 0}$
$\left( {a = 1,\;b = -3,\;c = 2} \right)$
The equation of the form $a + b + c = 0$
$ \Rightarrow $ The equation has two solutions ${x_1} = 1$, ${x_2} = \dfrac{2}{1} = 2$
8) ${{x^2} - 4x - 5 = 0}$
$\left( {a = 1,\;b = -4,\;c = -5} \right)$
The equation of the form $a - b + c = 0$
$ \Rightarrow $ The equation has two solutions ${x_1} = -1$, ${x_2} = \dfrac{{ - \left( { - 5} \right)}}{1} = 5$
Saturday, March 19, 2016
ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 1990$-$1991
Bài 1.
1) Giải hệ phương trình $\begin{cases}2x + 3y = 1\\x - 3y = 2\end{cases}$
2) Tính $\dfrac{1}{{\sqrt 5 - \sqrt 2 }} + \dfrac{1}{{\sqrt 5 + \sqrt 2 }}$
Bài 1.
1) Giải hệ phương trình $\begin{cases}2x + 3y = 1\\x - 3y = 2\end{cases}$
2) Tính $\dfrac{1}{{\sqrt 5 - \sqrt 2 }} + \dfrac{1}{{\sqrt 5 + \sqrt 2 }}$
3) Giải bất phương trình $\left( {x - 1} \right)\left( {2x + 3} \right) > 2x\left( {x + 3} \right)$
Bài 2. Trong mặt phẳng tọa độ, đơn vị trên hai
trục bằng nhau.
1) Xác định a để đồ thị hàm số $y = a{x^2}$ đi qua điểm A(1; 1). Vẽ đồ thị (P) của hàm số vừa tìm được. Hàm số này đồng biến, nghịch biến trên khoảng nào?
2) Gọi (D) là đường thẳng đi qua A và cắt trục Ox tại điểm M có hoành độ là (m $ \ne $ 1). Viết phương trình của đường thẳng (D).
3) Tìm giá trị của m để (D) chỉ có chung với (P) một điểm.
1) Xác định a để đồ thị hàm số $y = a{x^2}$ đi qua điểm A(1; 1). Vẽ đồ thị (P) của hàm số vừa tìm được. Hàm số này đồng biến, nghịch biến trên khoảng nào?
2) Gọi (D) là đường thẳng đi qua A và cắt trục Ox tại điểm M có hoành độ là (m $ \ne $ 1). Viết phương trình của đường thẳng (D).
3) Tìm giá trị của m để (D) chỉ có chung với (P) một điểm.
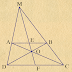
Bài 3. Cho đường tròn (O) cố định, BC là một
dây cung cố định của đường tròn (O), A là điểm di động trên cung lớn BC sao cho
tam giác ABC có ba góc nhọn. BB’ và CC’ là hai đường cao của tam giác ABC.
1)
Chứng minh bốn điểm B, C’, B’, C cùng nằm trên một đường tròn. Xác định đường
tròn đó.
2)
Chứng minh rằng AB.AC’ = AC.AB’.
3)
M là điểm chính giữa cung nhỏ BC của đường tròn (O). Tìm tập hợp trung điểm N của
AM khi A di động.
Friday, March 18, 2016
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2014$-$2015 QUẬN 11 TPHCM
Bài 1. (3 điểm) Giải các phương trình và hệ phương trình sau:
Bài 1. (3 điểm) Giải các phương trình và hệ phương trình sau:
a) $\begin{cases}3x - y = 7\\x + y = 1\end{cases}$
b) ${x^2} - 5x + 6 = 0$
c) ${x^2} - 4\sqrt 5 x + 20 = 0$
d) $2{x^4} + 5{x^2} - 7 = 0$
Bài 2. (1,5 điểm)
Cho hàm số: $y = {x^2}$ có đồ thị là (P) và đường thẳng (d): $y = -2x + 3$
a) Vẽ hai đồ thị (P) và (d) trên cùng một hệ trục tọa độ Oxy.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.
Bài 3. (2 điểm)
Cho phương trình: ${x^2} - 2\left( {m - 2} \right)x - 8 = 0$ (1) (x là ẩn số)
a) Chứng tỏ phương trình (1) luôn có 2 nghiệm với mọi giá trị của m.
b) Tìm tổng và tích 2 nghiệm của phương trình (1) theo m.
c) Tìm giá trị của m để 2 nghiệm ${x_1}$, ${x_2}$ của phương trình (1) thỏa:
$x_1^3 + x_2^3 - 4{x_1} - 4{x_2} = 0$
Bài 4. (3,5 điểm)
Cho $\triangle$ABC
nhọn (AB < AC). Đường tròn tâm O đường kính BC cắt AC, AB lần lượt tại E, F.
Gọi H là giao điểm của BE và CF.
a) Tính số đo
các góc BFC, BEC và chứng minh tứ giác AEHF nội tiếp.
b) Tia AH cắt BC
tại D và cắt (O) tại 2 điểm M, N (M nằm giữa A, H). Chứng minh $\triangle$BDH
và $\triangle$BEC
đồng dạng, từ đó suy ra $BH.BE = B{N^2}$.
c) Tiếp tuyến
tại F của (O) cắt AH tại I. Chứng minh tứ giác IEOD nội tiếp.
d)
Chứng minh: $\dfrac{{HM}}{{AM}} = \dfrac{{HD}}{{ND}}$.
Thursday, March 17, 2016
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2013$-$2014 QUẬN 11 TPHCM
Bài 1. (3 điểm) Giải các phương trình và hệ phương trình sau:
Bài 1. (3 điểm) Giải các phương trình và hệ phương trình sau:
a) $\begin{cases}2x - y = 2\\3x + 2y = 3\end{cases}$
b) ${x^2} - 5x + 6 = 0$
c) ${x^2} - 2\sqrt 3 x - 6 = 0$
d) $2{x^4} + 3{x^2} - 2 = 0$
Bài 2. (1,5 điểm)
Cho hàm số: $y = {x^2}$ có đồ thị là (P) và đường thẳng (D): $y = -x + 2$
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ Oxy.
b) Bằng phép tính hãy tìm tọa độ giao điểm của (P) và (D).
b) Bằng phép tính hãy tìm tọa độ giao điểm của (P) và (D).
Bài 3. (2 điểm)
Cho phương trình: ${x^2} - \left( {2m - 1} \right)x + 2m - 2 = 0$ (x là ẩn số)
a) Giải phương trình với m = 1.
b)
c) Gọi ${x_1}$, ${x_2}$ là hai nghiệm của phương trình. Tìm giá trị của m để biểu thức $A = x_1^2 + x_2^2$ đạt giá trị nhỏ nhất.
Cho phương trình: ${x^2} - \left( {2m - 1} \right)x + 2m - 2 = 0$ (x là ẩn số)
a) Giải phương trình với m = 1.
b)
c) Gọi ${x_1}$, ${x_2}$ là hai nghiệm của phương trình. Tìm giá trị của m để biểu thức $A = x_1^2 + x_2^2$ đạt giá trị nhỏ nhất.
Bài 4. (3,5 điểm)
Cho $\triangle$ABC
nhọn (AB < AC) nội tiếp trong đường tròn tâm O. Các đường cao BE, CF giao
nhau tại H.
a) Chứng minh: tứ
giác BCEF nội tiếp được trong đường tròn, xác định tâm I của đường tròn này.
b) Hai đường thẳng
EF và BC cắt nhau tại M. Chứng minh: MF.ME = MB.MC.
c) AM cắt đường
tròn (O) tại K. Chứng minh: tứ giác KFEA nội tiếp.
d)
Chứng minh: 3 điểm K, H, I thẳng hàng.
Wednesday, March 16, 2016
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2012$-$2013 QUẬN 11 TPHCM
Bài 1. (3 điểm) Giải các phương trình và hệ phương trình sau:
Bài 1. (3 điểm) Giải các phương trình và hệ phương trình sau:
a) $3{x^2} + 8x - 3 = 0$
b) $\begin{cases}3x + 6y = 1\\2x - 3y = 3\end{cases}$
b) $\begin{cases}3x + 6y = 1\\2x - 3y = 3\end{cases}$
c) ${x^2} - 4\sqrt 3 x + 12 = 0$
d) $3{x^4} + {x^2} - 1 = 0$
Bài 2. (1,5 điểm)
Cho hàm số: $y = {x^2}$ có đồ thị là (P) và đường thẳng (D): y = 2x + 3
a) Vẽ (P) và (D) trên cùng một hệ trục tọa độ Oxy.
b) Bằng phép tính hãy tìm tọa độ giao điểm của (P) và (D).
b) Bằng phép tính hãy tìm tọa độ giao điểm của (P) và (D).
Bài 3. (2 điểm)
Cho phương trình: ${x^2} - \left( {m + 2} \right)x + 2m = 0$ (x là ẩn số)
a) Giải phương trình với m = 1.
b)
c) Tìm m để phương trình có 2 nghiệm ${x_1}$, ${x_2}$ thỏa mãn $x_1^2 + {x_1}{x_2} + x_2^2 > 7$
Cho phương trình: ${x^2} - \left( {m + 2} \right)x + 2m = 0$ (x là ẩn số)
a) Giải phương trình với m = 1.
b)
c) Tìm m để phương trình có 2 nghiệm ${x_1}$, ${x_2}$ thỏa mãn $x_1^2 + {x_1}{x_2} + x_2^2 > 7$
Bài 4. (3,5 điểm)
Cho $\triangle$ABC
nhọn (AB < AC) nội tiếp trong đường tròn tâm O. Các đường cao AD, BE, CF
giao nhau tại H.
a)
Chứng minh tứ giác BFEC nội tiếp được trong đường tròn, xác định tâm I của đường
tròn này.
b)
Chứng minh: AE.BC = AB.EF.
c)
Gọi M là trung điểm của EF, N là giao điểm của OA và EF. Chứng minh: $\triangle$ANM
và $\triangle$ADI
đồng dạng.
d)
Chứng minh các đường thẳng AI, OH và trung tuyến BK của $\triangle$ABC
đồng qui.
Subscribe to:
Posts (Atom)
Popular Posts
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Hình thang cân 1. Hình thang có hai góc kề một đáy bằng nhau là hìn... -
$\boxed{\text {Bổ đề hình thang: }}$ Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điể... -
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TAM GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Tam giác cân 1. Tam giác có hai cạnh bằng nhau là tam giác cân.... -
$\boxed{\text {Bài toán 1: }}$ (Đề thi HKII 2008-2009 Q11 TpHCM) Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF c...
-
$\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ ABC. Chứng minh rằng... -
Để tìm ƯCLN, BCNN của các số tự nhiên, người ta thường dùng những cách sau: Cách 1 : Phân tích các số ra thừa số nguyên tố Vd: Tìm ƯC... -
Bạn cần download tài liệu, ebook,... phục vụ cho việc học tập nghiên cứu từ các trang Scribd, Issuu, Slideshare và Academia một cách nhanh...
-
Chương trình Tìm Ước chung lớn nhất và Bội chung nhỏ nhất của một dãy các số tự nhiên import java.util.Scanner; public class Main ...
-
Chương trình chuyển đổi một số tự nhiên ở hệ thập phân thành số ở hệ nhị phân, bát phân, thập lục phân và hệ cơ số bất kì import java.u...
-
Dãy số Fibonacci được định nghĩa như sau: F[0] =1, F[1] = 1; F[n] = F[n-1] + F[n-2] với n>=2. Hãy viết chương trình tìm số Fibonacci thứ ...