[HÌNH HỌC 8] BỔ ĐỀ HÌNH THANG

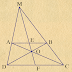
$\boxed{\text {Bổ đề hình thang: }}$

Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điểm của hai đường chéo và trung điểm của hai đáy cùng nằm trên một đường thẳng.

Chứng minh.

Cách 1: Gọi giao điểm của AD và BC là M, giao điểm của AC và BD là O, trung điểm của AB và CD lần lượt là E và F.

$\triangle$OAB $\sim$ $\triangle$OCD (g – g)

$ \Rightarrow $ $\dfrac{{AB}}{{CD}} = \dfrac{{AO}}{{CO}}$

$ \Rightarrow $ $\dfrac{{2AE}}{{2CF}} = \dfrac{{AO}}{{CO}}$

$ \Rightarrow $ $\dfrac{{AE}}{{CF}} = \dfrac{{AO}}{{CO}}$

$\triangle$OAE $\sim$ $\triangle$OCF (c – g – c)

$ \Rightarrow $ $\widehat {AOE} = \widehat {COF}$

mà $\widehat {AOE} + \widehat {EOC} = {180^0}$

$ \Rightarrow $ $\widehat {COF} + \widehat {EOC} = {180^0}$

$ \Rightarrow $ $\widehat {EOF} = {180^0}$

$ \Rightarrow $ E, O, F thẳng hàng (1)

Mặt khác, $\triangle$MAB $\sim$ $\triangle$MDC (g – g)

$ \Rightarrow $ $\dfrac{{AB}}{{CD}} = \dfrac{{MA}}{{MD}}$

$ \Rightarrow $ $\dfrac{{2AE}}{{2DF}} = \dfrac{{MA}}{{MD}}$

$ \Rightarrow $ $\dfrac{{AE}}{{DF}} = \dfrac{{AM}}{{DM}}$

$\triangle$MAE $\sim$ $\triangle$MDF (c – g – c)

$ \Rightarrow $ $\widehat {AME} = \widehat {DMF}$

$ \Rightarrow $ M, E, F thẳng hàng     (2)

(1), (2) $ \Rightarrow $M, E, O, F thẳng hàng

Cách 2:

Gọi giao điểm của AD và BC là M, giao điểm của AC và BD là O, giao điểm của MO và AB là E, giao điểm của MO và CD là F.

Ta có:

EB // DF $ \Rightarrow $ $\dfrac{{EB}}{{DF}} = \dfrac{{OB}}{{OD}}$    (1)

AE // DF $ \Rightarrow $ $\dfrac{{AE}}{{DF}} = \dfrac{{MA}}{{MD}}$    (2)

AB // CD $ \Rightarrow $ $\dfrac{{OB}}{{OD}} = \dfrac{{AB}}{{CD}}$ và $\dfrac{{MA}}{{MD}} = \dfrac{{AB}}{{CD}}$    (3)

(1), (2), (3) $ \Rightarrow $ $\dfrac{{AE}}{{DF}} = \dfrac{{EB}}{{DF}}$

$ \Rightarrow $ AE = EB

$ \Rightarrow $ E là trung điểm AB

Ta lại có:

$\dfrac{{AE}}{{DF}} = \dfrac{{EB}}{{FC}}\left( { = \dfrac{{ME}}{{MF}}} \right)$ (theo bài toán Chùm đường thẳng)

mà AE = EB (cmt)

$ \Rightarrow $ DF = FC

$ \Rightarrow $ F là trung điểm CD

* Lưu ý: Do không soạn được kí hiệu đồng dạng như trong SGK của VN nên tôi thay bằng kí hiệu đồng dạng "$\sim$" trong bài viết.