ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 1997$-$1998

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 1997$-$1998

Bài 1.

a) Tìm tất cả các giá trị của biểu thức $\sqrt {2x - 1} $ có nghĩa.

b) Giải hệ phương trình $\begin{cases}x + 2y = -4\\3x + 5y = 1\end{cases}$

c) Rút gọn $\dfrac{1}{{3 - \sqrt 2 }} + \dfrac{1}{{3 + \sqrt 2 }}$

Bài 2. Cho hàm số $y =  - {x^2}$ có đồ thị (P) và $y = 2x + m$ có độ thị (D) trên cùng một hệ trục tọa độ.

a) Vẽ đồ thị (P).

b) Định m để (D) và (P) có điểm chung duy nhất. Vẽ (D) với m vừa tìm được.

Bài 3.

a) Rút gọn biểu thức $M = \left( {\dfrac{1}{{1 - \sqrt a }} - \dfrac{1}{{1 + \sqrt a }}} \right)\left( {1 - \dfrac{1}{{\sqrt a }}} \right)$ với a $\ne$ 1, a > 0.

b) Tính giá trị của M khi $a = \dfrac{1}{9}$

Bài 4. Cho nửa đường tròn (O) đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) và tiếp tuyến thứ ba tiếp xúc với (O) tại điểm M cắt Ax tại D, cắt By tại E.

a) Chứng minh tam giác DOE là tam giác vuông.
b) Chứng minh $AD.BE = {R^2}$

c) Xác định vị trí của M trên nửa đường tròn (O) sao cho diện tích tam giác DOE đạt giá trị nhỏ nhất.

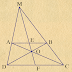
Bài 5. Cho tam giác ABC có đường phân giác trong BE hợp với cạnh AC một góc $45^0$ $\left( {\widehat {BEA} = {{45}^0}} \right)$. Vẽ đường cao AD của tam giác ABC. Chứng minh $\widehat {EDC} = {45^0}$.