Friday, July 15, 2022
On 8:30 PM by MATH CHANNEL in Đại số 9 No comments
I. ĐỊNH LÍ
Với $a,b \ge 0$, ta có: $\sqrt {a \cdot b} = \sqrt a \cdot \sqrt b $ .
Ví dụ: Tính
1) $\sqrt {81 \cdot 64} = \sqrt {81} \cdot \sqrt {64} = 9 \cdot 8 = 72$
2) $\sqrt {12 \cdot 3} = \sqrt {36} = 6$
II. ÁP DỤNG
a) Qui tắc khai phương một tích:
Ví dụ: Rút gọn
$\sqrt 8 - 2\sqrt {18} + \dfrac{3}{4}\sqrt {32} $
$= \sqrt {4 \cdot 2} - 2\sqrt {9 \cdot 2} + \dfrac{3}{4}\sqrt {16 \cdot 2}$
$ = 2\sqrt 2 - 2 \cdot 3\sqrt 2 + \dfrac{3}{4} \cdot 4\sqrt 2 $
$ = 2\sqrt 2 - 6\sqrt 2 + 3\sqrt 2 $
$= - \sqrt 2 $.
b) Qui tắc nhân các căn bậc hai:
Ví dụ: Tính
$\sqrt {\sqrt {10} - 1} \cdot \sqrt {\sqrt {10} + 1} = \sqrt {\left( {\sqrt {10} - 1} \right)\left( {\sqrt {10} + 1} \right)} = \sqrt {10 - 1} = \sqrt 9 = 3$
❄ Tổng quát: $\sqrt {A \cdot B} = \sqrt A \cdot \sqrt B $ $\left( {A,B \ge 0} \right)$.
Subscribe to:
Post Comments (Atom)
Search
Popular Posts
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Hình thang cân 1. Hình thang có hai góc kề một đáy bằng nhau là hìn...
-
$\boxed{\text {Bổ đề hình thang: }}$ Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điể...
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TAM GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Tam giác cân 1. Tam giác có hai cạnh bằng nhau là tam giác cân....
-
$\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ ABC. Chứng minh rằng...
-
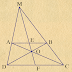
$\boxed{\text {Bài toán 1: }}$ (Đề thi HKII 2008-2009 Q11 TpHCM) Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF c...
-
Để tìm ƯCLN, BCNN của các số tự nhiên, người ta thường dùng những cách sau: Cách 1 : Phân tích các số ra thừa số nguyên tố Vd: Tìm ƯC...
-
Bạn cần download tài liệu, ebook,... phục vụ cho việc học tập nghiên cứu từ các trang Scribd, Issuu, Slideshare và Academia một cách nhanh...
-
Chương trình Tìm Ước chung lớn nhất và Bội chung nhỏ nhất của một dãy các số tự nhiên import java.util.Scanner; public class Main ...
-
Dãy số Fibonacci được định nghĩa như sau: F[0] =1, F[1] = 1; F[n] = F[n-1] + F[n-2] với n>=2. Hãy viết chương trình tìm số Fibonacci thứ ...
-
Chương trình Chuyển đổi một số tự nhiên ở hệ thập phân thành số ở hệ nhị phân, bát phân, thập lục phân và hệ cơ số bất kì import java.u...
Recent Posts
Categories
- Công nghệ thông tin
- Đại số 10
- Đại số 7
- Đại số 8
- Đại số 9
- Đề thi Toán 6
- Đề thi Toán 7
- Đề thi Toán 8
- Đề thi Toán 9
- Đố Toán
- Grade 6 Math
- Grade 8 Math
- Grade 9 Math
- Hình học 6
- Hình học 7
- Hình học 8
- Hình học 9
- Khác
- Lập trình Java cơ bản
- Math Puzzles
- Mathematical game
- Phương pháp học Toán
- Số học 6
- Số và Đại số 6
- Toán tham khảo 6
- Toán tham khảo 8
- Toán tham khảo 9
- Toán thực tế
- Toán và cuộc sống
Số lượt xem
Hỗ Trợ Trực Tuyến
Vườn Toán - Tin học. Powered by Blogger.









0 comments:
Post a Comment