ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2019$-$2020

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2019$-$2020

Bài 1. (1,5 điểm)
Cho parabol (P): $y =  - \dfrac{1}{2}x^2 $ và đường thẳng (d): $y = x - 4$.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2. (1,0 điểm)
Cho phương trình: $2x^2  - 3x - 1 = 0$ có 2 nghiệm là $x_1, x_2$.

Không giải phương trình, hãy tính giá trị của biểu thức $A = \dfrac{{x_1  - 1}}{{x_2  + 1}} + \dfrac{{x_2  - 1}}{{x_1  + 1}}$

Bài 3. (0,75 điểm)

Qui tắc sau đây cho ta biết được ngày $n$, tháng $t$, năm 2019 là ngày thứ mấy trong tuần.
    Đầu tiên, ta tính giá trị của biểu thức $T = n + H$, ở đây $H$ được xác định bởi bảng sau:

     Sau đó, lấy $T$ chia cho 7 ta được số dư $r$ $\left( {0 \le r \le 6} \right)$.

      Nếu $r = 0$ thì ngày đó là ngày thứ Bảy.

      Nếu $r = 1$ thì ngày đó là ngày Chủ Nhật.

      Nếu $r = 2$ thì ngày đó là ngày thứ Hai.

      Nếu $r = 3$ thì ngày đó là ngày thứ Ba.

      …

      Nếu $r = 6$ thì ngày đó là ngày thứ Sáu.

Ví dụ:

+ Ngày 31/12/2019 có $n$ = 31; $t$ = 12; $H$ = 0 $\Rightarrow$ $T$ = 31 + 0 = 31; số 31 chia cho 7 có số dư là 3, nên ngày đó là thứ Ba.

a) Em hãy sử dụng quy tắc trên để xác định các ngày 02/9/2019 va 20/11/2019 là thứ mấy?

b) Bạn Hằng tổ chức sinh nhật của mình trong tháng 10/2019. Hỏi sinh nhật của bạn Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai.

Bài 4. (0,75 điểm)

Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất y (atm) và độ sâu x (m) dưới mặt nước là một hàm số bậc nhất có dạng y = a + b.

a) Xác định các hệ số a và b.

b) Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất là 2,85 atm?

Bài 5. (1,0 điểm)

Một nhóm gồm 31 bạn học sinh tổ chức một chuyến đi du lịch (chi phí chuyến đi được chia đều cho mỗi bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việc đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí chuyến đi là bao nhiêu?

Bài 6. (1,0 điểm)

Cuối năm học, các bạn lớp 9A chia làm hai nhóm, mỗi nhóm chọn một khu vườn sinh thái ở Bắc bán cầu để tham quan. Khi mở hệ thống định vị GPS, họ phát hiện một sự trùng hợp khá thú vị là hai vị trí mà hai nhóm chọn đều nằm trên cùng một kinh tuyến và lần lượt ở các vĩ tuyến 47$^o$ và 72$^o$.

a) Tính khoảng cách (làm tròn đến hàng trăm) giữa hai vị trí đó, biết rằng kinh tuyến là một cung tròn nối liền hai cực của trái đất và có độ dài khoảng 20000 km.

b) Tính (làm tròn đến hàng trăm) độ dài bán kính và đường xích đao của trái đất. Từ kết quả của bán kính (đã làm tròn), hãy tính thể tích của trái đất, biết rằng trái đất có dạng hình cầu và thể tích của hình cầu được tính theo công thức $V = \dfrac{4}{3}.3,14.R^3 $ với $R$ là bán kính hình cầu.

Bài 7. (1,0 điểm)

Bạn Dũng trung bình tiêu thụ 15 ca-lo cho mỗi phút bơi và 10 ca-lo cho mỗi phút chạy bộ. Hôm nay, Dũng mất 1,5 giờ cho cả hai hoạt động trên và tiêu thụ hết 1200 ca-lo. Hỏi hôm nay, bạn Dũng mất bao nhiêu thời gian cho mỗi hoạt động?

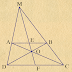
Bài 8. (3,0 điểm) Cho tam giác nhọn $ABC$ ($AB < AC$) nội tiếp đường tròn ($O$). Hai đường cao $BD$ và $CE$ của tam giác $ABC$ cắt nhau tại $H$. Đường thẳng $AH$ cắt $BC$ và ($O$) lần lượt tại $F$ và $K$ (K $\ne$ A). Gọi $L$ là hình chiếu của $D$ lên $AB$.

a) Chứng minh rằng tứ giác $BEDC$ nội tiếp và $BD^2  = BL.BA$.

b) Gọi $J$ là giao điểm của $KD$ và ($O$) (J $\ne$ K). Chứng minh $\widehat{BJK} = \widehat{BDE}$.

c) Gọi $I$ là giao điểm của $BJ$ và $ED$. Chứng minh tứ giác $ALIJ$ nội tiếp và $I$ là trung điểm của $ED$.