Showing posts with label Grade 6 Math. Show all posts
Showing posts with label Grade 6 Math. Show all posts
Tuesday, July 19, 2016
On 9:07 PM by MATH CHANNEL in Grade 6 Math 5 comments
I. THE NUMBER OF ELEMENTS IN A SET
$A = \left\{ 2 \right\}$ has 1 element
$B = \left\{ {a,b} \right\}$ has 2 elements
$C = \left\{ {1;2;3; \ldots ;100} \right\}$ has 100 elements
$\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}$ has infinite elements
* Note: The set which has no elements is called the emty set and is denoted by $\large\varnothing$
Example: $M=\left\{ x\in\mathbb{N} / x + 5 = 2 \right\} = \large\varnothing$
* Comment: A set may have one element, many elements, infinite elements, and may be no elements.
II. SUBSET
If every element in set E belongs to set F, then set E is called the subset of set F, and is denoted by: E $\subset$ F (hay F $\supset$ E)
Example 1: Given $E = \left\{ {a,b} \right\}$, $F = \left\{ {a,b,c,d} \right\}$
We have:
Example 2:
$M = \left\{ {1;5} \right\}$
$A = \left\{ {1;3;5} \right\}$
$B = \left\{ {5;1;3} \right\}$
We have: M $\subset$ A, M $\subset$ B
A $\subset$ B, B $\subset$ A
* Note: A $\subset$ B, B $\subset$ A hence A = B
Thursday, July 7, 2016
On 7:26 AM by MATH CHANNEL in Grade 6 Math 2 comments
I. SET $\mathbb{N}$ AND SET $\mathbb{N}^*$
_ The set of natural numbers is denoted by $\mathbb{N}$.
_ Every naturral number is represented by a point on the number ray. The point representing the natural number a on the number ray is called point a.
_ The set of non-zero natural number is denoted by $\mathbb{N}^*$.
$\mathbb{N}^*$ = {1; 2; 3; 4; 5; ...} or $\mathbb{N}^*$ = $\left\{ x\in\mathbb{N} / x \ne 0 \right\}$
II. THE ORDER
IN THE NATURAL NUMBER SET
_ Of two point on a number ray (number ray is horizontal with the direction of the arrow going from left to right), left point represents the smaller number.
_ Write a $\le$ b to show that a < b or a = b. And write a $\ge$ b to show that a > b or a = b.
_ If a < b và b < c then a < c.
_ Two consecutive natural numbers have a difference by one unit.
_ Number 0 is the smallest natural number. There is no greatest natural number.
_ The set of natural numbers has an infinite number of elements.III. WRITING NATURAL NUMBERS
_ A natural number can have one, two, three, etc digit(s).
Example: Number 5 has one digit.
Number 1005 has four digits.
_
In the decimal number system, ten units in one place make one unit in the
preceding place.
Example: $555 = 5.100 + 5.10 + 5$
$\overline {ab} = a.10 + b$ (a $\ne$ 0)
$\overline {abc} = a.100 + b.10 + c$ (a $\ne$ 0)
Saturday, July 2, 2016
On 1:53 AM by MATH CHANNEL in Grade 6 Math 1 comment
I. EXAMPLES
_ Set of
students of class 6A
_ Set of letters a, b, c
_ Set of one digit even numbers
…………
II. WRITING
METHOD. NOTATIONS
Sets are
usually named with capital letters.
Example: Set of one
digit even numbers.
A = $ \left\{ {0;2;4;6;8} \right\}$
Set of
words cam and chanh.
B = $ \left\{ {cam,\;chanh} \right\}$
0; 2; 4; 6; 8
cam, chanh
Notations: 2 $\in$ A (2 belongs to A), ổi $\notin$ B (ổi does not belong to B)
►Note:
_ Elements of a set are written in two braces { } which are separated by “;” (if its
elements are numbers) or by
To write a set, we usually use two ways:
_ Listing elements of the set.
_ Showing
characteristic properties of the set.
Example: Write down the set A of natural numbers greater than 8 and less than 14 by two ways, the fill each square with a suitable notation.
Way 1: A = $ \left\{ {9;10;11;12;13} \right\}$
Way 2: A = $\left\{ x\in\mathbb{N} / 8<x<14 \right\}$
12 $\boxed{\in}$ A, 16 $\boxed{\notin}$ A
Saturday, April 16, 2016
On 9:57 PM by MATH CHANNEL in Grade 6 Math 1 comment
I. METHOD OF MEASURING ANGLE
To measure angle xOy, a protractor is placed so that its center coincides with vertex O of the angle, one side of the angle (such Ox) passes through line 0 of the protractor. Assume that the other side of the angle (ray Oy) passes through line 33. Then we say measurement of angle xOy is 33 degrees.
The measurement of angle xOy is 33 degrees, is denoted by $\widehat {xOy} = {33^0}$ or $\angle xOy = {33^0}$
(Tâm của thước: Center of a protractor)
The measurement of angle xOy is 33 degrees, is denoted by $\widehat {xOy} = {33^0}$ or $\angle xOy = {33^0}$
(Tâm của thước: Center of a protractor)
II. PRACTICE MEASURING ANGLES
Find the measurement of the angles in below figures?
Both angles are $139^0$
You can practice more at website http://www.mathplayground.com/measuringangles.html

Tuesday, March 29, 2016
On 2:21 AM by MATH CHANNEL in Grade 6 Math 1 comment
I. RATIO OF TWO NUMBERS
_ The quotient in the division of number $a$ by number $b$ ($b$ $ \ne $ 0) is called the ratio of $a$ to $b$.
_ The ratio of $a$ to $b$ is denoted by $a$ : $b$ or $\dfrac{a}{b}$.
Example: 1.7 : 3.12; $\dfrac{1}{5}:\dfrac{3}{4}$; $ - 3\dfrac{1}{4}:5$; ... are ratios.
* Note: When we say ratio $\dfrac{a}{b}$, then $a$ and $b$ can be integers, fractions, mixed numbers, …, on the other hand, for fraction $\dfrac{a}{b}$, both $a$ and $b$ must be integers.
_ The ratio of $a$ to $b$ is denoted by $a$ : $b$ or $\dfrac{a}{b}$.
Example: 1.7 : 3.12; $\dfrac{1}{5}:\dfrac{3}{4}$; $ - 3\dfrac{1}{4}:5$; ... are ratios.
* Note: When we say ratio $\dfrac{a}{b}$, then $a$ and $b$ can be integers, fractions, mixed numbers, …, on the other hand, for fraction $\dfrac{a}{b}$, both $a$ and $b$ must be integers.
II. PERCENTAGE
Rule: To find the percentage of $a$ to $b$, we compute $\dfrac{{a.100}}{b}\% $.
Example: Find the percentage of:
a) $5$ và $8$
The percentage of $5$ to $8$ is:
$\dfrac{5}{8} = \dfrac{{5 \times 100}}{8}\% = 62.5\% $
b) 25kg và $\dfrac{3}{{10}}$quintal
$\dfrac{3}{{10}}$quintal = $\dfrac{3}{{10}}$ $\times$ 100kg = 30kg
The percentage of 25kg to $\dfrac{3}{{10}}$quintal is:
$\dfrac{{25}}{{30}} = \dfrac{5}{6} = \dfrac{{5 \times 100}}{6}\% = 83.3\% $
III. SCALE
Scale $T$ of a drawing (or a map) is the
ratio of distance $a$ between two points on the drawing (or the map) to distance $b$ between two points in corresponding reality: $T = \dfrac{a}{b}$ (a, b have the
same unit of measurement).
Example: If the
distance $a$ on a map is 1cm, the actual distance $b$ is 1km, the map scale $T$ is 1
: 100000.
Saturday, March 5, 2016
On 6:50 AM by MATH CHANNEL in Grade 6 Math 1 comment
\[\boxed{\text {Is this true: }\dfrac{9}{4} = 2\dfrac{1}{4} = 2.25 = 225\% \text { ? }}\]
I. MIXED NUMBERS
Example: 7 divided by 4 is 1 with remainder 3.
Then, we write: $\boxed{\dfrac{7}{4} = 1 + \dfrac{3}{4} = 1\dfrac{3}{4}}$. The number $1\dfrac{3}{4}$ is a mixed number, where 1 is the integer part and $\dfrac{3}{4}$ is the fraction part of $\dfrac{7}{4}$.
❄ Covert mixed numbers to fractions
$5\dfrac{1}{7} = \dfrac{{5.7 + 1}}{7} = \dfrac{{36}}{7}$
$\dfrac{7}{3} = 2\dfrac{1}{3}$ (7 divided by 3 is 2 with remainder 1)
$5\dfrac{1}{7} = \dfrac{{5.7 + 1}}{7} = \dfrac{{36}}{7}$
$ - 4\dfrac{3}{5}$ = $\bf-$$\dfrac{{4.5 + 3}}{5}$ = $\bf-$$\dfrac{{23}}{5}$
❄ Covert fractions to mixed numbers$\dfrac{7}{3} = 2\dfrac{1}{3}$ (7 divided by 3 is 2 with remainder 1)
$\dfrac{ - 7}{4}$ = $\bf-$$\dfrac{7}{4}$ = $\bf-$$ 1 \dfrac{3}{4}$
II. DECIMAL NUMBERS
- A decimal fraction is a fraction where the denominator is a power of 10 (such as: $\dfrac{3}{{10}}$, $\dfrac{{ - 152}}{{100}}$, $\dfrac{{73}}{{1000}}$, etc).
- The decimal fractions can be written as decimal numbers.
- A decimal number includes two parts:
+ Integer part is written on the left of the decimal separator,
+ Decimal part is written on the right of the decimal separator.
Example: $\dfrac{3}{{10}} = \color{black}{0.3}$; $\dfrac{-152}{{100}} = \color{black}{-1.52}$; $\dfrac{73}{{1000}} = \color{black}{0.073}$; etc are fractions.
- The number of digits in the decimal part is exactly equal to the number of 0 digits in the denominator of the decimal fraction.
❄ Covert decimal fractions to decimal numbers:
$\dfrac{{27}}{{100}} = 0.27$
$\dfrac{{ - 13}}{{1000}} = - 0.013$
$\dfrac{{261}}{{100000}} = 0.00261$
❄ Covert decimal numbers to decimal fractions:
$1.21 = \dfrac{{121}}{{100}}$
$0.07 = \dfrac{{7}}{{100}}$
$-2.013 = \dfrac{{-2013}}{{1000}}$
Fractions with denominator 100 are written as percentages with the symbol %.
Example: $\dfrac{3}{{100}} = 3\% $
$\dfrac{107}{{100}} = 107\% $
$\dfrac{7}{{25}} = \dfrac{{28}}{{100}} = 28\% $
$\dfrac{{26}}{{65}} = \dfrac{2}{5} = \dfrac{{40}}{{100}} = 40\% $
$3.7 = \dfrac{{37}}{{10}} = \dfrac{{370}}{{100}} = 370\% $
$0.34 = \dfrac{{34}}{{100}} = 34\% $
❄ Covert percentages to decimal numbers
$7\% = 0.07$
$45\% = 0.45$
$216\% = 2.16$
Friday, March 4, 2016
On 5:41 AM by MATH CHANNEL in Grade 6 Math 1 comment
I. ADDITION OF FRACTIONS
❄ Adding two fractions with the same denominator $\boxed{\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}}$
❄ Adding two fractions with different denominators: We just convert fractions to the same denominator and applies the above rule.
Example: Calculate:
1) $\dfrac{3}{8} + \dfrac{5}{8} = \dfrac{{3 + 5}}{8} = \dfrac{8}{8} = 1$
2) $\dfrac{1}{7} + \dfrac{{ - 4}}{7} = \dfrac{{1 + ( - 4)}}{7} = \dfrac{{ - 3}}{7}$
3) $\dfrac{6}{{18}} + \dfrac{{ - 14}}{{21}} = \dfrac{1}{3} + \dfrac{{ - 2}}{3} = \dfrac{{1 + ( - 2)}}{3} = \dfrac{{ - 1}}{3}$
4) $\dfrac{{ - 2}}{3} + \dfrac{4}{{15}} = \dfrac{{ - 10}}{{15}} + \dfrac{4}{{15}} = \dfrac{{ - 6}}{{15}} = \dfrac{{ - 2}}{5}$
5) $\dfrac{{11}}{{15}} + \dfrac{9}{{ - 10}} = \dfrac{{11}}{{15}} + \dfrac{{ - 9}}{{10}} = \dfrac{{22}}{{30}} + \dfrac{{ - 27}}{{30}} = \dfrac{{ - 5}}{{30}} = \dfrac{{ - 1}}{6}$
6) $\dfrac{1}{{ - 7}} + 3 = \dfrac{{ - 1}}{7} + \dfrac{3}{1} = \dfrac{{ - 1}}{7} + \dfrac{{21}}{7} = \dfrac{{20}}{7}$
Similarly as the addition of intergers, the addition of fractions has the following fundamental properties:
a) Commutative property: $\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{c}{d} + \dfrac{a}{b}$
b) Associative property: $\left( {\dfrac{a}{b} + \dfrac{c}{d}} \right) + \dfrac{p}{q} = \dfrac{a}{b} + \left( {\dfrac{c}{d} + \dfrac{p}{q}} \right)$
c) Adding to numer 0: $\dfrac{a}{b} + 0 = 0 + \dfrac{a}{b} = \dfrac{a}{b}$
❄ Adding two fractions with different denominators: We just convert fractions to the same denominator and applies the above rule.
Example: Calculate:
1) $\dfrac{3}{8} + \dfrac{5}{8} = \dfrac{{3 + 5}}{8} = \dfrac{8}{8} = 1$
2) $\dfrac{1}{7} + \dfrac{{ - 4}}{7} = \dfrac{{1 + ( - 4)}}{7} = \dfrac{{ - 3}}{7}$
3) $\dfrac{6}{{18}} + \dfrac{{ - 14}}{{21}} = \dfrac{1}{3} + \dfrac{{ - 2}}{3} = \dfrac{{1 + ( - 2)}}{3} = \dfrac{{ - 1}}{3}$
4) $\dfrac{{ - 2}}{3} + \dfrac{4}{{15}} = \dfrac{{ - 10}}{{15}} + \dfrac{4}{{15}} = \dfrac{{ - 6}}{{15}} = \dfrac{{ - 2}}{5}$
5) $\dfrac{{11}}{{15}} + \dfrac{9}{{ - 10}} = \dfrac{{11}}{{15}} + \dfrac{{ - 9}}{{10}} = \dfrac{{22}}{{30}} + \dfrac{{ - 27}}{{30}} = \dfrac{{ - 5}}{{30}} = \dfrac{{ - 1}}{6}$
6) $\dfrac{1}{{ - 7}} + 3 = \dfrac{{ - 1}}{7} + \dfrac{3}{1} = \dfrac{{ - 1}}{7} + \dfrac{{21}}{7} = \dfrac{{20}}{7}$
Similarly as the addition of intergers, the addition of fractions has the following fundamental properties:
a) Commutative property: $\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{c}{d} + \dfrac{a}{b}$
b) Associative property: $\left( {\dfrac{a}{b} + \dfrac{c}{d}} \right) + \dfrac{p}{q} = \dfrac{a}{b} + \left( {\dfrac{c}{d} + \dfrac{p}{q}} \right)$
c) Adding to numer 0: $\dfrac{a}{b} + 0 = 0 + \dfrac{a}{b} = \dfrac{a}{b}$
II. SUBTRACTION OF FRACTIONS
Rule: $\boxed{\dfrac{a}{b} \color{red}{-} \dfrac{c}{d} = \dfrac{a}{b} \color{red}{+} \left( {\dfrac{{ - c}}{d}} \right)}$
Note: $\boxed{\dfrac{a}{{ - b}} = - \dfrac{a}{b} = \dfrac{{ - a}}{b}}$
Example: Calculate:1) $\dfrac{1}{8} - \dfrac{1}{2} = \dfrac{1}{8} + \dfrac{{ - 1}}{2} = \dfrac{1}{8} + \dfrac{{ - 4}}{8} = \dfrac{{ - 3}}{8}$
2) $\dfrac{{ - 5}}{7} - \dfrac{1}{3} = \dfrac{{ - 5}}{7} + \dfrac{{ - 1}}{3} = \dfrac{{ - 15}}{{21}} + \dfrac{{ - 7}}{{21}} = \dfrac{{ - 22}}{{21}}$
3) $\dfrac{3}{5} - \dfrac{{ - 1}}{2} = \dfrac{3}{5} + \dfrac{1}{2} = \dfrac{6}{{10}} + \dfrac{5}{{10}} = \dfrac{{11}}{{10}}$
4) $\dfrac{{ - 2}}{5} - \dfrac{{ - 3}}{4} = \dfrac{{ - 2}}{5} + \dfrac{3}{4} = \dfrac{{ - 8}}{{20}} + \dfrac{{15}}{{20}} = \dfrac{7}{{20}}$
5) $ - 5 - \dfrac{1}{6} = \dfrac{{ - 5}}{1} + \dfrac{{ - 1}}{6} = \dfrac{{ - 30}}{6} + \dfrac{{ - 1}}{6} = \dfrac{{ - 31}}{6}$
III. MULTIPLICATION OF FRACTIONS
Rule: $\boxed{\dfrac{a}{b} . \dfrac{c}{d} = \dfrac{{a . c}}{c . d}}$
Example: Calculate:
1) $\dfrac{{ - 3}}{7}.\dfrac{2}{{ - 5}} = \dfrac{{( - 3).2}}{{7.( - 5)}} = \dfrac{{ - 6}}{{ - 35}} = \dfrac{6}{{35}}$
2) $\dfrac{{ - 28}}{{33}}.\dfrac{{ - 3}}{4} = \dfrac{{( - 28).( - 3)}}{{33.4}} = \dfrac{{\color{red}{28}.\color{blue}{3}}}{{\color{blue}{33}.\color{red}{4}}} = \dfrac{{\color{red}{7}.\color{blue}{1}}}{{\color{blue}{11}.\color{red}{1}}} = \dfrac{7}{{11}}$
3) ${\left( {\dfrac{{ - 3}}{5}} \right)^2} = \dfrac{{ - 3}}{5}.\dfrac{{ - 3}}{5} = \dfrac{9}{{25}}$
4) ${\left( { - \dfrac{3}{2}} \right)^5} = \left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right) = - \dfrac{{{3^5}}}{{{2^5}}} = - \dfrac{{243}}{{32}}$
5) $( - 2).\dfrac{{ - 3}}{7} = \dfrac{{( - 2).( - 3)}}{7} = \dfrac{6}{7}$ $\left(a.\dfrac{b}{c} \color{orange}{ = \dfrac{a}{1}.\dfrac{b}{c}} = \dfrac{{a.b}}{c}\right)$
6) $\dfrac{5}{{33}}.(-3) = \dfrac{{5.\color{red}{( - 3)}}}{\color{red}{33}} = \dfrac{{5.\color{red}{( - 1)}}}{\color{red}{11}} = \dfrac{{ - 5}}{{11}}$ $\left(\dfrac{a}{b}.c \color{orange}{ = \dfrac{a}{b}.\dfrac{c}{1}} = \dfrac{{a.c}}{b}\right)$
Similarly as the multiplication of intergers, the multiplication of fractions has the following fundamental properties:
a) Commutative property: $\dfrac{a}{b} . \dfrac{c}{d} = \dfrac{c}{d} . \dfrac{a}{b}$
b) Associative property: $\left( {\dfrac{a}{b} . \dfrac{c}{d}} \right) . \dfrac{p}{q} = \dfrac{a}{b} . \left( {\dfrac{c}{d} . \dfrac{p}{q}} \right)$
c) Multiplying by number 1: $\dfrac{a}{b} . 1 = 1 . \dfrac{a}{b} = \dfrac{a}{b}$
d) Distributive property of multiplication over addition: $\dfrac{a}{b}.\left( {\dfrac{c}{d} \pm \dfrac{p}{q}} \right) = \dfrac{a}{b}.\dfrac{c}{d} \pm \dfrac{a}{b}.\dfrac{p}{q}$
IV. DIVISION OF FRACTIONS
Rule: $\boxed{\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b}.\dfrac{d}{c} = \dfrac{{a.d}}{{b.c}}\;\left( {c \ne 0} \right)}$
Example: Calculate:
1) $\dfrac{5}{6}:\dfrac{{ - 7}}{{12}} = \dfrac{5}{6}.\dfrac{{ - 12}}{7} = \dfrac{5}{1}.\dfrac{{ - 2}}{7} = \dfrac{{ - 10}}{7}$
2) $ - 7:\dfrac{{14}}{3} = - 7.\dfrac{3}{{14}} = \dfrac{{ - 3}}{2}$
3) $\dfrac{{ - 3}}{7}:9 = \dfrac{{ - 3}}{7}.\dfrac{1}{9} = \dfrac{{ - 1}}{7}.\dfrac{1}{3} = \dfrac{{ - 1}}{{21}}$
Wednesday, March 2, 2016
On 7:26 AM by MATH CHANNEL in Grade 6 Math 1 comment
❄ COMPARING TWO FRACTIONS
To compare two fractions, we do as follows:
Way 2: Compare two fractions with suitable numbers (integers or fractions).Note:
1) The fraction in which numerator and denominator have the same sign integers is greater than 0. A fraction greater than 0 is called a positive fraction. Conversely, the fraction in which numerator and denominator have the different sign integers is less than 0. A fraction less than 0 is called a negative fraction.
2) For a positive fraction (numerator and denominator have the same sign), if the numerator is greater than the denominator, the fraction is greater than 1 and conversely.
3) Of two positive fractions with the same numerator, the fraction with the smaller denominator is the larger fraction and conversely.
4) Given two fractions $\dfrac{a}{b}$ and $\dfrac{c}{d}$ (a, b, c, d $\in$ $\mathbb{N}^*$, a < c, b > d) then $\dfrac{a}{b} < \dfrac{c}{b} < \dfrac{c}{d}$
5) When we just want to know if two fractions are equivalent, we apply the following property $\dfrac{a}{b} = \dfrac{c}{d} \Leftrightarrow a.d = b.c$
Example 1: Are the follwing pairs of fractions equivalent?
1) $\dfrac{2}{3}$ and $\dfrac{6}{9}$
$\dfrac{2}{3} = \dfrac{6}{9}$ since 2.9 = 3.6
2) $\dfrac{{ - 3}}{4}$ and $\dfrac{5}{{ - 7}}$
$\dfrac{{ - 3}}{4} \ne \dfrac{5}{{ - 7}}$ since $( - 3).( - 7) \ne 4.5$
Example 2: Compare the following fractions:
1) $\dfrac{14}{{21}}$ and $\dfrac{ - 60}{{ - 72}}$
$\dfrac{{14}}{{21}} = \dfrac{{2}}{{3}}$, $\dfrac{{ - 60}}{{ - 72}} = \dfrac{{5}}{{6}}$
CD = 6
$\dfrac{2}{3} = \dfrac{{2.2}}{{3.2}} = \dfrac{4}{6}$
Since $\dfrac{{4}}{{6}} < \dfrac{{ 5}}{6}$,
$\dfrac{{14}}{{21}} < \dfrac{{ - 60}}{ - 72}$
2) $\dfrac{-2}{{7}}$ and $\dfrac{24}{{-56}}$
$\dfrac{{24}}{{ - 56}} = \dfrac{{ - 3}}{{7}}$ (divide both the numerator and denominator by $-$8)
Since $\dfrac{{-2}}{{7}} > \dfrac{{ - 3}}{7}$,
$\dfrac{{-2}}{{7}} > \dfrac{{24}}{-56}$
3) $\dfrac{11033}{{15045}}$ and $\dfrac{1111}{{1515}}$
$\dfrac{{11033}}{{15045}} = \dfrac{{11}}{{15}}$ (divide both the numerator and denominator by 1003)
$\dfrac{{1111}}{{1515}} = \dfrac{{11}}{{15}}$ (divide both the numerator and denominator by 101)
So, $\dfrac{{11033}}{{15045}} = \dfrac{{1111}}{{1515}}$
4) $\dfrac{141}{{893}}$ and $\dfrac{159}{{901}}$
$\dfrac{{141}}{{893}} = \dfrac{3}{{19}}$, $\dfrac{{159}}{{901}} = \dfrac{3}{{17}}$
Since $\dfrac{{3}}{{19}} < \dfrac{{3}}{17}$,
$\dfrac{{141}}{{893}} < \dfrac{{159}}{901}$
5) $\dfrac{ - 19}{{7}}$ and $\dfrac{1}{{6}}$
$\dfrac{{ - 19}}{7} < 0 < \dfrac{1}{6}$
$ \Rightarrow $ $\dfrac{{ - 19}}{7} < \dfrac{1}{6}$
6) $\dfrac{{79}}{{97}}$ and $\dfrac{71}{{17}}$
$\dfrac{{79}}{97} < 1 < \dfrac{71}{17}$
$ \Rightarrow $ $\dfrac{{79}}{97} < \dfrac{71}{17}$
7) $\dfrac{{37}}{{195}}$ and $\dfrac{73}{{179}}$
$\dfrac{{37}}{{195}} < \dfrac{{73}}{{195}} < \dfrac{{73}}{{179}}$
$ \Rightarrow $ $\dfrac{{37}}{{195}} < \dfrac{{73}}{{179}}$
8) $\dfrac{{12}}{{29}}$ and $\dfrac{16}{{41}}$
$\dfrac{{12}}{{29}} > \dfrac{{12}}{{30}} = \dfrac{2}{5} = \dfrac{{16}}{{40}} > \dfrac{{16}}{{41}}$
$ \Rightarrow $ $\dfrac{{12}}{{29}} > \dfrac{{16}}{{41}}$
9) $\dfrac{{22}}{{7}}$ and $\dfrac{34}{{11}}$
$\dfrac{{22}}{7} = 3\dfrac{1}{7}\;\left( { = 3 + \dfrac{1}{7}} \right)$, $\dfrac{{34}}{{11}} = 3\dfrac{1}{{11}}\;\left( { = 3 + \dfrac{1}{{11}}} \right)$
Since $\dfrac{{1}}{{7}} > \dfrac{{1}}{11}$,
$\dfrac{{22}}{{7}} > \dfrac{{34}}{11}$
Sunday, February 28, 2016
On 9:59 PM by MATH CHANNEL in Grade 6 Math 1 comment
❄ CONVERTING MANY FRACTIONS TO THE SAME DENOMINATOR
To convert many fractions to the same denominator, we do as follows:
Step 1: Reduce the given fractions, convert their negative denomonators to positive denominators.
Step 2: Find a common denominator (usually LCM)
Step 3: Multiply numerator and denominator of each fraction by corresponding sub-factor (find sub-factor by dividing the common denominator by each denominator)
Step 1: Reduce the given fractions, convert their negative denomonators to positive denominators.
Step 2: Find a common denominator (usually LCM)
Step 3: Multiply numerator and denominator of each fraction by corresponding sub-factor (find sub-factor by dividing the common denominator by each denominator)
Example: Convert the following fractions to the same denominator:
$\dfrac{-4}{{7}}$, $\dfrac{16}{{18}}$ and $\dfrac{20}{{-42}}$
Solution:
$\dfrac{{16}}{{18}} = \dfrac{{8}}{{9}}$, $\dfrac{{20}}{{-42}} = \dfrac{{-10}}{{21}}$
In order to find a common denominator, we often use the following ways:
Way 2: In the three denominators 7, 9, 21, we get the greatest denominator that is 21. We'll multiply 21 by 1, 2, 3, etc until receiving the answer which is divisible by the remaining numbers, that receiving answer is a common denominator. In this case, 21 $\times$ 3 = 63 is divisible by 7, 9, 21. Thus, 21 is common denominator which we have to find.
CD = 63
The 1st sub-factor 63 : 7 = 9, the 2nd sub-factor 63 : 9 = 7, the 3rd sub-factor 63 : 21 = 3
$\dfrac{{ - 4}}{7} = \dfrac{{ - 4.9}}{{7.9}} = \dfrac{{ - 36}}{{63}}$
$\dfrac{8}{9} = \dfrac{{8.7}}{{9.7}} = \dfrac{{56}}{{63}}$
$\dfrac{{ - 10}}{{21}} = \dfrac{{ - 10.3}}{{21.3}} = \dfrac{{ - 30}}{{63}}$
Saturday, February 27, 2016
On 7:11 AM by MATH CHANNEL in Grade 6 Math 1 comment
Rule: In order to reduce a fraction, divide the numerator and denominator by their divisor (other than 1 and $-$1).
$\dfrac{a}{b} = \dfrac{{a : n}}{{b : n}}$ where $n$ $ \in $ CD($a$, $b$)
Note:
_ Fractions in lowest terms (or fractions which can not be reduced further) are fractions such that their numerator and denominator have only 1 and $-$1 as common divisors.
$\dfrac{a}{b} = \dfrac{{a : n}}{{b : n}}$ where $n$ $ \in $ CD($a$, $b$)
Note:
_ Fractions in lowest terms (or fractions which can not be reduced further) are fractions such that their numerator and denominator have only 1 and $-$1 as common divisors.
$\dfrac{a}{b}$ is $a$ fraction in lowest terms $ \Leftrightarrow $ CD($a$, $b$) = $\left\{ { \pm 1} \right\}$
_ When reducing a fraction, we often reduce it to the fraction in lowest terms and has positive denominator.
II. EXAMPLES
Example: Reduce the following fractions:
$\dfrac{{6}}{{8}} = \dfrac{3}{4}$ (divide both the numerator and denominator by 2)
$\dfrac{{ - 5}}{{10}} = \dfrac{{ - 1}}{2}$ (divide both the numerator and denominator by 5)
$\dfrac{{18}}{{ - 33}} = \dfrac{{ - 6}}{{11}}$ (divide both the numerator and denominator by $-$3)
$\dfrac{{ - 36}}{{ - 12}} = \dfrac{3}{1} = 3$ (divide both the numerator and denominator by $-$12)
Subscribe to:
Posts (Atom)
Search
Popular Posts
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Hình thang cân 1. Hình thang có hai góc kề một đáy bằng nhau là hìn...
-
$\boxed{\text {Bổ đề hình thang: }}$ Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điể...
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TAM GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Tam giác cân 1. Tam giác có hai cạnh bằng nhau là tam giác cân....
-
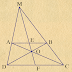
$\boxed{\text {Bài toán 1: }}$ (Đề thi HKII 2008-2009 Q11 TpHCM) Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF c...
-
$\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ ABC. Chứng minh rằng...
-
Để tìm ƯCLN, BCNN của các số tự nhiên, người ta thường dùng những cách sau: Cách 1 : Phân tích các số ra thừa số nguyên tố Vd: Tìm ƯC...
-
Bạn cần download tài liệu, ebook,... phục vụ cho việc học tập nghiên cứu từ các trang Scribd, Issuu, Slideshare và Academia một cách nhanh...
-
Chương trình Tìm Ước chung lớn nhất và Bội chung nhỏ nhất của một dãy các số tự nhiên import java.util.Scanner; public class Main ...
-
Dãy số Fibonacci được định nghĩa như sau: F[0] =1, F[1] = 1; F[n] = F[n-1] + F[n-2] với n>=2. Hãy viết chương trình tìm số Fibonacci thứ ...
-
Chương trình chuyển đổi một số tự nhiên ở hệ thập phân thành số ở hệ nhị phân, bát phân, thập lục phân và hệ cơ số bất kì import java.u...
Recent Posts
Categories
- Công nghệ thông tin
- Đại số 10
- Đại số 7
- Đại số 8
- Đại số 9
- Đề thi Toán 6
- Đề thi Toán 7
- Đề thi Toán 8
- Đề thi Toán 9
- Đố Toán
- Grade 6 Math
- Grade 8 Math
- Grade 9 Math
- Hình học 6
- Hình học 7
- Hình học 8
- Hình học 9
- Khác
- Lập trình Java cơ bản
- Math Puzzles
- Mathematical game
- Phương pháp học Toán
- Số học 6
- Số và Đại số 6
- Toán tham khảo 6
- Toán tham khảo 8
- Toán tham khảo 9
- Toán thực tế
- Toán và cuộc sống
My Fanpage
Số lượt xem
Hỗ Trợ Trực Tuyến
Vườn Toán - Tin học. Powered by Blogger.