[HÌNH HỌC 9] CÁC BÀI TOÁN TỔNG HỢP VỀ HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

$\boxed{\text {Bài toán 1: }}$ Cho $\triangle$ABC vuông tại A có đường cao AH, AD là đường phân giác góc A. Biết BH = 9cm, AB = 15cm.

a) Tính độ dài AH, AC, BC.

b) Tính cosB, $\tan\widehat {CAH}$.

c) Tính độ dài BD.

d) Qua D kẻ đường thẳng vuông góc với BC cắt cạnh AC tại E. Chứng minh: BD = DE. Suy ra $\sin \widehat {BED}$.

$\boxed{\text {Bài toán 2: }}$ Cho $\triangle$ABC vuông tại A có đường cao AH, AD là trung tuyến. Biết BC = 25cm, AB = 20cm.

a) Tính độ dài BH, AH, AC

b) Tính sinB, cotC

c) Kẻ đường thẳng đi qua H và song song với AD, đường thẳng này cắt cạnh AC tại I và cắt đường thẳng AB tại K. Chứng minh: AK.AC = AB.AI

d) Chứng minh: HI + HK = 2AD

$\boxed{\text {Bài toán 3: }}$ Cho $\triangle$ABC vuông tại A có đường cao AH. Biết AC = 16cm, AB = 12cm.

a) Tính độ dài BC, AH, CH.

b) Tính sinB, tanC, $\cot \widehat {BAH}$.

c) Tia phân giác góc B cắt AC tại D. Tính độ dài BD.
d) Chứng minh: $\tan \dfrac{{\widehat {ABC}}}{2} = \dfrac{{AC}}{{AB + BC}}$

$\boxed{\text {Bài toán 4: }}$ Cho $\triangle$ABC vuông tại A có đường cao AH. Biết AC = 20cm, AB = 15cm.

a) Tính độ dài BC, AH.

b) Gọi M là trung điểm của HC. Tính sinB, $\tan \widehat {HAM}$.

c) Vẽ tia phân giác AD của $\triangle$AHB (D $\in$ BH). Chứng minh: $\triangle$ACD cân.

d) Gọi I là trung điểm của AH, đường thẳng BI cắt AM, AC lần lượt tại E, F. Chứng minh: BE.BF = BH.BC.

$\boxed{\text {Bài toán 5: }}$ Cho $\triangle$ABC vuông tại A, đường cao AH chia cạnh huyền BC thành 2 đoạn BH = 9cm, HC = 16cm.

a) Tính độ dài AH và tanC.

b) Từ H vẽ HD, HE lần lượt vuông góc với AB, AC (D $\in$ AB, E $\in$ AC). Chứng minh: ADHE là hình chữ nhật và AB.AD = AC.AE .

c) Tia ED cắt AH tại O và cắt tia CB tại F. Tính tỉ số $\dfrac{{FD}}{{FC}}$.

d) Đường thẳng vuông góc với DE vẽ từ D cắt BC tại M. Chứng minh: AM $\bot$ CO.

$\boxed{\text {Bài toán 6: }}$ Cho $\triangle$ABC vuông tại A có AB = 15cm, AC = 20cm, đường cao AH. Gọi E, F lần lượt là trung điểm của AH và BH.

a) Tính độ dài BC, AH, CH.

b) Tính sinB, tanECH. Từ đó tính số đo góc ECH (làm tròn đến độ).

c) CE cắt AF, AB lần lượt tại I và K, EF cắt AC tại N. Chứng minh tam giác CIB đồng dạng tam giác CHK.

d) Tính độ dài EN.

$\boxed{\text {Bài toán 7: }}$ Cho $\triangle$ABC vuông tại A, đường cao AH, trung tuyến AM. Biết AB = 15cm, AC = 20cm.

a) Tính độ dài BC, AM.

b) Tính $\sin \widehat {AMH}$, số đo $\widehat {HAM}$ (làm tròn đến độ).

c) Đường thẳng vuông góc với AM vẽ từ C cắt tia AH tại F. Chứng minh rằng tia FM đi qua trung điểm N của AC.

d) Gọi I là trực tâm của $\triangle$ABM. Chứng minh rằng điểm đối xứng với điểm B qua I nằm trên AC.

$\boxed{\text {Bài toán 8: }}$ Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Vẽ BH vuông góc với đường chéo AC (H $\in$ AC)

a) Tính độ dài AC, BH.

b) Tính $\sin \widehat {HBC}$, $\dfrac{{\tan \widehat {ABH}}}{{\cot \widehat {ACB}}}$.

c) Gọi M, N, K lần lượt là trung điểm của AH, AB, CD. BK cắt AC tại I. Chứng minh: đường thẳng DI đi qua trung điểm F của BC.

d) Chứng minh: $\widehat {BMK} = {90^0}$. 

Read More

[Arithmetic 6] The number of elements in a set. Subset

I. THE NUMBER OF ELEMENTS IN A SET

$A = \left\{ 2 \right\}$ has 1 element

$B = \left\{ {a,b} \right\}$ has 2 elements

$C = \left\{ {1;2;3; \ldots ;100} \right\}$ has 100 elements

$\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}$ has infinite elements

* Note: The set which has no elements is called the emty set and is denoted by $\large\varnothing$

   Example: $M=\left\{ x\in\mathbb{N} / x + 5 = 2 \right\} = \large\varnothing$

* Comment: A set may have one element, many elements, infinite elements, and may be no elements.

II. SUBSET

If every element in set E belongs to set F, then set E is called the subset of set F, and is denoted by: E $\subset$ F (hay F $\supset$ E)

Example 1: Given $E = \left\{ {a,b} \right\}$, $F = \left\{ {a,b,c,d} \right\}$

            We have: E $\subset$ F (or F $\supset$ E)

Example 2: 

        $M = \left\{ {1;5} \right\}$

        $A = \left\{ {1;3;5} \right\}$

        $B = \left\{ {5;1;3} \right\}$

We have: M $\subset$ A, M $\subset$ B

          A $\subset$ B, B $\subset$ A

* Note: A $\subset$ B, B $\subset$ A hence A = B

Read More

[SỐ HỌC 6] SỐ PHẦN TỬ CỦA MỘT TẬP HỢP. TẬP HỢP CON

I. SỐ PHẦN TỬ CỦA MỘT TẬP HỢP
$A = \left\{ 2 \right\}$ có 1 phần tử

$B = \left\{ {a,b} \right\}$ có 2 phần tử

$C = \left\{ {1;2;3; \ldots ;100} \right\}$ có 100 phần tử

$\mathbb{N} = \left\{ {0;1;2;3; \ldots } \right\}$ có vô số phần tử

* Chú ý: Tập hợp không có phần tử nào gọi là tập hợp rỗng, kí hiệu: $\large\varnothing$

   Ví dụ: $M=\left\{ x\in\mathbb{N} / x + 5 = 2 \right\} = \large\varnothing$

* Nhận xét: Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào.

II. TẬP HỢP CON

Nếu mọi phần tử của tập hợp E đều thuộc tập hợp F thì tập hợp E gọi là tập hợp con của tập hợp F, kí hiệu: E $\subset$ F (hay F $\supset$ E)

Ví dụ 1: Cho $E = \left\{ {a,b} \right\}$, $F = \left\{ {a,b,c,d} \right\}$

            Ta có: E $\subset$ F (hay F $\supset$ E)

Ví dụ 2: 

        $M = \left\{ {1;5} \right\}$

        $A = \left\{ {1;3;5} \right\}$

        $B = \left\{ {5;1;3} \right\}$

Ta có: M $\subset$ A, M $\subset$ B

          A $\subset$ B, B $\subset$ A

* Chú ý: A $\subset$ B, B $\subset$ A suy ra A = B

Read More

[Arithmetic 6] Set of natural numbers

I. SET $\mathbb{N}$ AND SET $\mathbb{N}^*$

_ The set of natural numbers is denoted by $\mathbb{N}$.

$\mathbb{N}$ = {0; 1; 2; 3; 4; 5; ...}

_ Every naturral number is represented by a point on the number ray. The point representing the natural number a on the number ray is called point a.

_ The set of non-zero natural number is denoted by $\mathbb{N}^*$.

$\mathbb{N}^*$ = {1; 2; 3; 4; 5; ...} or $\mathbb{N}^*$ = $\left\{ x\in\mathbb{N} / x \ne 0 \right\}$

II. THE ORDER IN THE NATURAL NUMBER SET

_ Of two point on a number ray (number ray is horizontal with the direction of the arrow going from left to right), left point represents the smaller number.

_ Write a $\le$ b to show that a < b or a = b. And write a $\ge$ b to show that a > b or a = b.

_ If a < b và b < c then a < c.

_ Two consecutive natural numbers have a difference by one unit.

_ Number 0 is the smallest natural number. There is no greatest natural number.

_ The set of natural numbers has an infinite number of elements.

III. WRITING NATURAL NUMBERS

_ A natural number can have one, two, three, etc digit(s).

Example:  Number 5 has one digit.

                Number 1005 has four digits.

_ In the decimal number system, ten units in one place make one unit in the preceding place.

Example: $555 = 5.100 + 5.10 + 5$

               $\overline {ab}  = a.10 + b$  (a $\ne$ 0)

               $\overline {abc}  = a.100 + b.10 + c$ (a $\ne$ 0)

Read More

[SỐ HỌC 6] TẬP HỢP CÁC SỐ TỰ NHIÊN

I. TẬP HỢP $\mathbb{N}$ VÀ TẬP HỢP $\mathbb{N}^*$

_ Tập hợp các số tự nhiên, kí hiệu $\mathbb{N}$.

$\mathbb{N}$ = {0; 1; 2; 3; 4; 5; ...}

_ Mỗi số tự nhiên được biểu diễn bởi 1 điểm trên tia số. Điểm biểu diễn số tự nhiên a trên tia số gọi là điểm a.

_ Tập hợp các số tự nhiên khác 0, kí hiệu $\mathbb{N}^*$.

$\mathbb{N}^*$ = {1; 2; 3; 4; 5; ...} hay $\mathbb{N}^*$ = $\left\{ x\in\mathbb{N} / x \ne 0 \right\}$

II. THỨ TỰ TRONG TẬP HỢP SỐ TỰ NHIÊN

_ Trong 2 điểm trên tia số (tia số nằm ngang, chiều mũi tên đi từ trái sang phải) điểm ở bên trái biểu diễn số nhỏ hơn.

_ Viết a $\le$ b tức là a < b hay a = b. Viết a $\ge$ b tức là a > b hay a = b.

_ Nếu a < b và b < c thì a < c.

_ Hai số tự nhiên liên tiếp hơn kém nhau 1 đơn vị.

_ Số 0 là số tự nhiên nhỏ nhất, không có số tự nhiên lớn nhất.

_ Tập hợp các số tự nhiên có vô số phần tử.

III. GHI SỐ TỰ NHIÊN
_ Một số tự nhiên có thể có một, hai, ba,... hay nhiều chữ số.

Ví dụ:  Số 5 có 1 chữ số

            Số 1005 có 4 chữ số

_ Trong hệ thập phân, cứ 10 đơn vị ở 1 hàng làm thành 1 đơn vị ở hàng liền trước nó.

Ví dụ: $555 = 5.100 + 5.10 + 5$

           $\overline {ab}  = a.10 + b$  (a $\ne$ 0)

           $\overline {abc}  = a.100 + b.10 + c$ (a $\ne$ 0)

Read More

[Arithmetic 6] Sets. Elements of a set

I. EXAMPLES

_ Set of students of class 6A

_ Set of letters a, b, c

_ Set of one digit even numbers

…………

II. WRITING METHOD. NOTATIONS

Sets are usually named with capital letters.

Example: Set of one digit even numbers.

A = $ \left\{ {0;2;4;6;8} \right\}$

Set of words cam and chanh.

B = $ \left\{ {cam,\;chanh} \right\}$

0; 2; 4; 6; 8  are elements of set A

cam, chanh are elements of set B.

Notations: 2 $\in$ A (2 belongs to A), ổi $\notin$ B (ổi does not belong to B)

►Note:

_ Elements of a set are written in two braces { } which are separated by “;” (if its elements are numbers) or by “,”.

_ Each element is listed once, with arbitrary oder of listing.

To write a set, we usually use two ways:

_ Listing elements of the set.

_ Showing characteristic properties of the set.

Example: Write down the set A of natural numbers greater than 8 and less than 14 by two ways, the fill each square with a suitable notation.

Way 1: A = $ \left\{ {9;10;11;12;13} \right\}$

Way 2: A = $\left\{ x\in\mathbb{N} / 8<x<14 \right\}$

12 $\boxed{\in}$ A, 16 $\boxed{\notin}$ A

The set is illustracted by a Venn diagram.

Read More

[SỐ HỌC 6] TOÁN NÂNG CAO VỀ SỐ TỰ NHIÊN

Bài toán 1: Cần dùng bao nhiêu chữ số để đánh số các trang của một quyển sách có 475 trang.

Bài toán 2: Để đánh số các trang của một quyển sách người ta phải dùng tất cả 900 chữ số, hỏi quyển sách có bao nhiêu trang?

Bài toán 3: Phải dùng bao nhiêu chữ số 3 để viết tất cả các số tự nhiên từ 1 đến 99?

Bài toán 4: Người ta viết liền nhau dãy các số tự nhiên liên tiếp bắt đầu từ 1. Hỏi chữ số thứ 629 là chữ số nào?

Bài toán 5: Người ta viết liền nhau dãy các số tự nhiên liên tiếp bắt đầu từ 1. Hỏi chữ số 4 của số 243 là chữ số thứ bao nhiêu?

Bài toán 6: Chứng tỏ rằng trong $\mathbb{N}$, tổng của số bị trừ, số trừ và hiệu bao giờ cũng là một số chẵn.

Bài toán 7: Một con chó đuổi một con thỏ cách nó 150dm. Một bước nhảy của chó dài 9dm, một bước nhảy của thỏ dài 7dm và khi chó nhảy một bước thì thỏ cũng nhảy một bước. Hỏi chó phải nhảy bao nhiêu bước mới đuổi kịp thỏ?

Bài toán 8: Ngày 01-05-2005 rơi vào ngày chủ nhật. Hỏi ngày 01-05-2017 rơi vào thứ mấy?

Bài toán 9: Chia 166 cho một số ta được số dư là 5. Chia 51 cho số đó ta cũng được số dư là 5. Tìm số chia.

Bài toán 10: Trong một phép chia có số bị chia là 235 số dư là 14. Tìm số chia và thương.

Bài toán 11: Chia một số cho 60 thì được số dư là 37. Nếu chia số đó cho 15 thì số dư là bao nhiêu? Thương thay đổi thế nào?

Bài toán 12: Lan và Cúc có tất cả 80 quyển sách. Sau khi Lan cho Cúc 3 quyển thì Lan còn hơn Cúc 10 quyển sách. Hỏi lúc đầu mỗi người có bao nhiêu quyển sách?

Bài toán 13: Một mảnh đất hình chữ nhật có chu vi là 130m. Nếu bớt chiều dài đi 4m và tăng chiều rộng thêm 5m thì chiều dài vẫn hơn chiều rộng là 6m. Tính diện tích của mảnh đất lúc ban đầu.

Bài toán 14: Tổng của hai số là 2756. Nếu thêm chữ số 2 vào bên trái số nhỏ thì được số lớn. Biết số nhỏ là một số có 3 chữ số, tìm hai số đó.

Bài toán 15: Tổng hai chữ số của một số có hai chữ số bằng 8. Nếu đổi chỗ hai chữ số cho nhau ta được một số mới nhỏ hơn số cũ là 18. Tìm số đó.

Bài toán 16: Một phép trừ có tổng của số bị trừ, số trừ và hiệu bằng 1890. Hiệu lớn hơn số trừ là 633. Tìm số bị trừ và số trừ.

Bài toán 17: Quãng đường AB dài 110km. Lúc 7 giờ, người thứ nhất đi từ A để đến B, người thứ hai đi từ B để đến A. Họ gặp nhau lúc 9 giờ. Biết vận tốc người thứ nhất lớn hơn vận tốc người thứ hai là 5km/h. Tính vận tốc mỗi người.

Bài toán 18: Một phép chia có tổng số chia và số bị chia bằng 160. Biết rằng thương là 3 và số dư là 12. Tìm số bị chia và số chia.

Bài toán 19: Đường sắt từ Hà Nội qua Nha Trang tới TP Hồ Chí Minh dài 1726km. Biết 3 lần khoảng cách Nha Trang – TP Hồ Chí Minh cộng thêm 82km nữa thì bằng khoảng cách Nha Trang – Hà Nội. Hỏi đường sắt từ Hà Nội tới Nha Trang dài bao nhiêu?

Bài toán 20: Hiệu của hai số là 283. Nếu lấy số lớn chia cho số nhỏ thì được thương là 5 và dư 3. Tìm hai số đó.

Bài toán 21: Thương của hai số là 15. Số lớn hơn số nhỏ là 532. Tìm số bị chia và số chia.

Bài toán 22: Hiện nay bà hơn cháu 52 tuổi. Sau 14 năm nữa thì bà gấp 3 lần tuổi cháu. Tính tuổi bà, tuổi cháu hiện nay.

Bài toán 23: Tôi có một tờ giấy to và xé nó ra làm 9 mảnh. Sau đó, lấy một số mảnh, xé mỗi mảnh thành 9 mảnh nhỏ, rồi trộn vào với các mảnh cũ. Tôi lại lấy một số mảnh trong đống giấy ấy, xé mỗi mảnh làm 9 mảnh rồi lại trộn vào với các mảnh cũ và cứ thế tiếp tục. Lúc sau tôi dừng lại và nhờ bạn tôi đếm số mảnh giấy có được, anh nói: 1968. Hãy chứng minh rằng anh ấy đếm... sai!

Bài toán 24: Hai người bộ hành nghỉ chân bên vệ đường, giở gói bánh bao ra ăn. Một người có năm chiếc, một người có ba chiếc. Họ cắt tàu lá chuối trải lên bãi cỏ, bỏ chung bánh vào cùng ăn. Bỗng có một người lái buôn vừa đi tới. Hai người mời người lái buôn cùng ăn với mình. Đang đói và thấy hai người mời niềm nở, khách không từ chối. Ba người cùng lần lượt ăn hết tám cái bánh. Cứ mỗi cái bánh được bẻ ra ba phần. Họ ăn xong cái này lại cắt tiếp cái khác. Ăn xong, người lái buôn vội đi, xin gởi lại tám đồng bạc. Hai người có bánh đem tiền ra chia. Người có năm cái bánh nhất quyết phải lấy năm đồng. Người có ba chiếc bánh đòi phải chia đôi số tiền. Hai người cãi nhau, bất phân thắng bại, đành đưa nhau đến cho quan sở tại phân xử.

    Nếu em là quan sở tại em sẽ chia số tiền trên cho hai người như thế nào?

Bài toán 25: Chứng tỏ $\left( {a + {a^2} + {a^3} + {a^4} +  \ldots  + {a^{2n}}} \right)\; \vdots \;\left( {a + 1} \right)$ với a, n $\in$ $\mathbb{N}$

Bài toán 26: Chứng tỏ $H = {5^1} + {5^2} + {5^3} +  \ldots  + {5^{60}}$ chia hết cho 31

Bài toán 27: Tìm số dư khi chia $A = 4 + {4^2} + {4^3} +  \ldots  + {4^{16}} + {4^{17}}$ cho 17

Bài toán 28: So sánh $A = 2 + {2^2} + {2^3} +  \ldots  + {2^{59}} + {2^{60}}$ và $B = {2^{61}}$

Bài toán 29: Có số tự nhiên nào chia cho 12 dư 9, chia cho 15 dư 1 không?

Bài toán 30: Điền vào dấu * các chữ số thích hợp để được phép tính đúng:
                                  * * * *
                              $\times$          9
                              -------------
                                2 1 1 8 *

Bài toán 31: Tìm hai số tự nhiên chia hết cho 9 biết tổng bằng $\overline {*730} $ và hiệu của chúng bằng $\overline {*638} $.

Bài toán 32: Tìm số tự nhiên n, biết:
1) $42\; \vdots \;2n$
2) $14\; \vdots \;\left( {2n + 3} \right)$
3) $\left( {4n + 5} \right)\; \vdots \;n$
4) $\left( {n + 5} \right)\; \vdots \;\left( {n + 1} \right)$
5) $\left( {3n + 4} \right)\; \vdots \;\left( {n - 1} \right)$

Bài toán 33: Hương đến quầy văn phòng phẩm mua 3 bút chì, 6 bút bi và 9 quyển vở (giá mỗi loại là số tự nhiên). Hương đưa chị bán hàng 2 tờ giấy bạc loại 20000 đồng. Chị bán hàng thối lại 5000 đồng. Hương nhận tiền và nói “Chị xem lại, chị đã tính nhầm rồi!” và đúng là chị bán hàng đã tính nhầm. Hương dựa vào đâu mà phát hiện nhanh quá vậy?

Bài toán 34: Chứng tỏ rằng các số sau là hợp số:
1) $191.1912.19123.191234 + 1$
2) $751.751752.751752753 - 11$
3) ${2^6}{.6^{101}} + 1$
4) ${10^{100}} - 7$
5) $\underbrace {111 \ldots 11}_{{\text{2007 chữ số 1}}}$
6) $\underbrace {111 \ldots 11}_{{\text{2006 chữ số 1}}}$

Bài toán 35: Tính độ dài cạnh của một hình vuông, biết diện tích của nó bằng 1794 $m^2$.

Bài toán 36: Mỗi số sau có bao nhiêu ước: 12 345 432 100 000; 4 225 000 000 000

Bài toán 37: Chứng minh các số sau đây nguyên tố cùng nhau:

a) Hai số tự nhiên liên tiếp.

b) Hai số lẻ liên tiếp.

c) Số 3n + 1 và 4n + 1 (n $\in$ $\mathbb{N}$)

Bài toán 38: Cho a và b là hai số nguyên tố cùng nhau và a > b. Chứng minh rằng ƯCLN(a, a + b) = 1

Bài toán 39: Khu vườn hình chữ nhật có chiều dài 300m, rộng 80m. Người ta trồng cây xung quanh vườn sao cho mỗi góc đều trồng 1 cây và khoảng cách hai cây liên tiếp bằng nhau và lớn nhất. Tính số cây phải trồng.

Bài toán 40: Một miếng bìa hình chữ nhật có chiều dài là 162cm và chiều rộng 108cm. Người ta tính cắt hết miếng bìa thành những hình vuông bằng nhau (độ dài cạnh là số tự nhiên). Hỏi cạnh của hình vuông lớn nhất là bao nhiêu và miếng bìa được cắt thành bao nhiêu hình vuông như thế?

Bài toán 41: Một căn phòng hình chữ nhật có chiều dài 7m, chiều rộng 5m được lát gạch hình vuông. Hàng cuối cùng sát chân hai bức tường liền nhau không thể để nguyên kích thước của viên gạch mà phải cắt xén bớt đi vì chiều dài còn dư ra 10cm, chiều rộng còn dư ra 20cm. Tính độ dài mỗi cạnh của viên gạch.

Bài toán 42: Khối 6, 7, 8 của một trường học lần lượt có 300, 276, 252 học sinh. Khi chào cờ, học sinh của 3 khối xếp số hàng dọc như nhau.

a) Có thể xếp được nhiều nhất bao nhiêu hàng dọc mà mỗi khối không lẻ hàng?

b) Lúc đó mỗi khối có bao nhiêu hàng ngang?

Bài toán 43: Có 3 chồng sách: Văn, Âm nhạc, Toán mỗi chồng sách chỉ gồm một loại sách. Mỗi cuốn sách Văn dày 15mm, mỗi cuốn Âm nhạc dày 6mm, mỗi cuốn Toán dày 8mm. Người ta xếp cho 3 chồng sách cao bằng nhau. Tính chiều cao nhỏ nhất của ba chồng sách đó.

Bài toán 44: Số học sinh khối 6 của một trường trong khoảng từ 500 đến 600 học sinh. Cho biết nếu học sinh xếp hàng 8 thì dư 7, hàng 12 dư 11, hàng 15 dư 14 học sinh. Tính số học sinh đó.

Bài toán 45: Tại một bến xe, cứ 10 phút lại có một chuyến taxi rời bến, cứ 12 phút lại có một chuyến xe buýt rời bến. Lúc 6 giờ, một xe taxi và một xe buýt cùng rời bến một lúc. Hỏi lúc mấy giờ lại có một taxi và một xe buýt cùng rời bến lần tiếp theo?

Bài toán 46: Hai anh em cùng đo khoảng cách giữa hai điểm A và B bằng bước chân. Mỗi bước của anh dài 54cm, của em dài 42cm. Họ cùng bước đi từ A và khi bước chân cuối cùng vừa đến B thì có đúng 50 lần bước chân của hai anh em trùng nhau. Tính khoảng cách AB.

Bài toán 47: Một bà mang một rổ trứng ra chợ. Dọc đường gặp một bà khác vô ý đụng phải, rổ trứng rơi xuống đất vỡ khơng cịn một quả. Bà kia tỏ ý muốn đền lại số trứng bèn hỏi:

- Bà cho biết trong rổ có bao nhiêu trứng?

Bà có rổ trứng trả lời:

- Tôi chỉ nhớ rằng số trứng đó chia cho 2, cho 3, cho 4, cho 5, cho 6 lần nào cũng còn thừa một quả nhưng chia cho 7 thì không thừa quả nào. À, mà số trứng chưa đến 400 quả.

Tính xem trong rổ có bao nhiêu trứng?

Read More

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2016$-$2017

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2016$-$2017

Bài 1. Giải các phương trình và hệ phương trình sau:

a) ${x^2} - 2\sqrt 5 x + 5 = 0$

b) $4{x^4} - 5{x^2} - 9 = 0$

c) $\begin{cases}2x + 5y = -1\\3x - 2y = 8\end{cases}$

d) $x\left( {x + 3} \right) = 15 - \left( {3x - 1} \right)$

Bài 2.

a) Vẽ đồ thị (P) của hàm số $y =  - {\dfrac{x}{4}^2}$ và đường thẳng (D): $y = \dfrac{x}{2} - 2$ trên cùng một hệ trục tọa độ.

b) Tìm tọa độ các giao điểm của (P) và (D) ở câu trên bằng phép tính.

Bài 3.

a) Thu gọn biểu thức sau: $A = \dfrac{{2 - \sqrt 3 }}{{1 + \sqrt {4 + 2\sqrt 3 } }} + \dfrac{{2 + \sqrt 3 }}{{1 - \sqrt {4 - 2\sqrt 3 } }}$

b) Ông Sáu gửi một số tiền vào ngân hàng theo mức lãi suất tiết kiệm với kỳ hạn 1 năm là 6%. Tuy nhiên sau thời hạn một năm ông Sáu không đến nhận tiền lãi mà để thêm một năm nữa mới lãnh. Khi đó số tiền lãi có được sau năm đầu tiên sẽ được ngân hàng cộng dồn vào số tiền gửi ban đầu để thành số tiền gửi cho năm kế tiếp với mức lãi suất cũ. Sau 2 năm ông Sáu nhận được số tiền là 112.360.000 đồng (kể cả gốc lẫn lãi). Hỏi ban đầu ông Sáu đã gửi bao nhiêu tiền?

Bài 4. Cho phương trình: ${x^2} - 2mx + m - 2 = 0$ (1) (x là ẩn số)

a) Chứng minh phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị m.

b) Định m để hai nghiệm $x_1$, $x_2$ của phương trình (1) thỏa mãn:

$\left( {1 + {x_1}} \right)\left( {2 - {x_2}} \right) + \left( {1 + {x_2}} \right)\left( {2 - {x_1}} \right) = x_1^2 + x_2^2 + 2$

Bài 5. Cho tam giác ABC (AB < AC) có ba góc nhọn. Đường tròn tâm O đường kính BC cắt các cạnh AC, AB lần lượt tại D, E. Gọi H là giao điểm của BD và CE; F là giao điểm của AH và BC.

a) Chứng minh: AF $\bot$ BC và $\widehat {AFD} = \widehat {ACE}$.

b) Gọi M là trung điểm của AH. Chứng minh: MD $\bot$ OD và 5 điểm M, D, O, F, E cùng thuộc một đường tròn.

c) Gọi K là giao điểm của AH và DE. Chứng minh: MD${^2}$ = MK.MF và K là trực tâm của tam giác MBC.

d) Chứng minh: $\dfrac{2}{{FK}} = \dfrac{1}{{FH}} + \dfrac{1}{{FA}}$.

Read More

[SỐ HỌC 6] TẬP HỢP - PHẦN TỬ CỦA TẬP HỢP

I. CÁC VÍ DỤ

_ Tập hợp các học sinh của lớp 6A.

_ Tập hợp chữ cái a, b, c.

_ Tập hợp các số chẵn có một chữ số.

…………

II. CÁCH VIẾT. CÁC KÍ HIỆU

    Tên tập hợp được đặt bằng chữ cái in hoa.

Ví dụ: Tập hợp các số chẵn có 1 chữ số.

$A = \left\{ {0;2;4;6;8} \right\}$

Tập hợp các chữ cam, chanh.

$B = \left\{ {cam,\;chanh} \right\}$

0; 2; 4; 6; 8  là các phần tử của A

cam, chanh là các phần tử của B.

Kí hiệu: 2 $\in$ A (2 thuộc tập A), ổi $\notin$ B (ổi không thuộc tập B)

Ví dụ: Viết tập hợp các chữ cái trong từ "GOOGLE".

$C = \left\{ {G;O;L;E} \right\}$

►Chú ý:

_ Các phần tử của một tập hợp được viết trong cặp dấu { } cách nhau bởi dấu “;” (nếu các phần tử là số) hoặc “,”.

_ Mỗi phần tử được liệt kê 1 lần theo thứ tự tùy ý.

Để viết tập hợp, thường có hai cách:

_ Liệt kê các phần tử của tập hợp.

_ Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.

Ví dụ: Viết tập hợp A các số tự nhiên lớn hơn 8 và nhỏ hơn 14 bằng hai cách, sau đó điền kí hiệu thích hợp vào ô vuông.

Cách 1: $A = \left\{ {9;10;11;12;13} \right\}$

Cách 2: $A=\left\{ x\in\mathbb{N} / 8<x<14 \right\}$

12 $\boxed{\in}$ A, 16 $\boxed{\notin}$ A

Minh họa tập hợp bằng biểu đồ Venn:

Read More

[HÌNH HỌC 9] ĐƯỜNG THẲNG EULER

$\boxed{\text {Bài toán: }}$

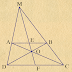
Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ABC. Chứng minh rằng O, H, G cùng thuộc một đường thẳng (được gọi là đường thẳng Euler của $\triangle$ABC) và GH = 2GO.

Giải

Chứng minh.

Cách 1:

Vẽ OM $\bot$ BC, ON $\bot$ AC

Ta có: M, N lần lượt là trung điểm của BC, AC (đ/lí đường kính vuông góc dây cung)

$ \Rightarrow $ MN là đường trung bình của $\triangle$ABC

$ \Rightarrow $ MN // AB

$ \Rightarrow $ $\widehat {NMC} = \widehat {ABC}$, $\widehat {MNC} = \widehat {BAC}$

$\widehat {OMN} + \widehat {NMC} = {90^0}$, $\widehat {HAB} + \widehat {ABC} = {90^0}$, $\widehat {NMC} = \widehat {ABC}$

$ \Rightarrow $ $\widehat {OMN} = \widehat {HAB}$

$\widehat {ONM} + \widehat {MNC} = {90^0}$, $\widehat {ABH} + \widehat {BAC} = {90^0}$, $\widehat {MNC} = \widehat {BAC}$

$ \Rightarrow $ $\widehat {ONM} = \widehat {ABH}$

$\triangle$OMN và $\triangle$HAB có: $\widehat {OMN} = \widehat {HAB}$ (cmt), $\widehat {ONM} = \widehat {ABH}$ (cmt)

$ \Rightarrow $ $\triangle$OMN $\sim$ $\triangle$HAB (g – g)

$ \Rightarrow $ $\dfrac{{OM}}{{HA}} = \dfrac{{MN}}{{AB}} = \dfrac{1}{2}$

$ \Rightarrow $ $OM = \dfrac{1}{2}HA$

Gọi G’ là giao điểm của AM và OH

OM // AH $ \Rightarrow $ $\dfrac{{G'M}}{{G'A}} = \dfrac{{OM}}{{HA}} = \dfrac{1}{2}$

$ \Rightarrow $ G’ là trọng tâm của $\triangle$ABC

$ \Rightarrow $ G’ $ \equiv $ G

Vậy H, G, O thẳng hàng và $\dfrac{{GO}}{{GH}} = \dfrac{{OM}}{{HA}} = \dfrac{1}{2}$

Cách 2:

Gọi M là trung điểm BC. Kẻ đường kính AD.

Ta có: $\widehat {ACD} = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$ \Rightarrow $ CD $\bot$ AC

mà BH $\bot$ AC

$ \Rightarrow $ BH // CD

Tương tự, CH // BD

BHCD là hình bình hành (hai cặp cạnh đối song song)

mà M là trung điểm của BC

$ \Rightarrow $ M là trung điểm HD

$\triangle$ABC có AM là đường trung tuyến (M là trung điểm BC), G là trọng tâm

$ \Rightarrow $ G $\in$ AM và $AG = \dfrac{2}{3}AM$

$\triangle$AHD có AM là đường trung tuyến (M là trung điểm HD), G $\in$ AM và $AG = \dfrac{2}{3}AM$

$ \Rightarrow $ G là trọng tâm của $\triangle$AHD

mà HO là đường trung tuyến của $\triangle$AHD

$ \Rightarrow $ G $\in$ HO và GH = 2GO

 Vậy O, H, G cùng thuộc một đường thẳng và GH = 2GO

* Lưu ý: Do không soạn được kí hiệu đồng dạng như trong SGK của VN nên tôi thay bằng kí hiệu đồng dạng "$\sim$" trong bài viết.

Read More