ĐỀ THI TOÁN 8 QUẬN 11 TPHCM

HKI

HKII

ĐỀ THI TOÁN 8 HỌC KÌ II NĂM HỌC 2008$-$2009 QUẬN 11 TPHCM

Read More

ĐỀ THI TOÁN 7 QUẬN 11 TPHCM

HKI

HKII

ĐỀ THI TOÁN 7 HỌC KÌ II NĂM HỌC 2008$-$2009 QUẬN 11 TPHCM

Read More

ĐỀ THI TOÁN 6 HỌC KÌ I NĂM HỌC 2019$-$2020 QUẬN 11 TPHCM

ĐỀ THI TOÁN 6 HỌC KÌ I NĂM HỌC 2019$-$2020 QUẬN 11 TPHCM

Bài 1. (2,5 điểm) Thực hiện phép tính:

a) $39.13 + 87.39$
b) $2^3 .4 + 5^6 :5^4  - 2019^0$
c) $260:\left\{ {120 - \left[ {24 + \left( {9 - 5} \right)^2 } \right]} \right\}$

Bài 2. (1,5 điểm) Tìm số tự nhiên x, biết:

a) $\left( {x - 20} \right) + 4 = 14$

b) $78 - 4x = 54$
c) $3\left( {x - 18} \right) + 20 = 41$

Bài 3. (1 điểm)
a) Sắp xếp các số nguyên sau theo thứ tự tăng dần: –32; 21; –2; 0; –2020

b) Tìm ƯCLN(70; 84)

Bài 4. (1 điểm) Mỗi ngày Mai được mẹ cho $30000$ đồng, Mai ăn sáng hết $20000$ đồng, Mai mua nước uống hết $5000$ đồng, phần tiền còn lại Mai để vào ống heo tiết kiệm. Hỏi sau 30 ngày, Mai có bao nhiêu tiền tiết kiệm?

Bài 5. (1 điểm) Một trường tổ chức cho học sinh khối 6 và 7 đi tham quan nông trại. Số học sinh khi xếp lên xe 40 chỗ hay 45 chỗ đều vừa đủ. Biết rằng số học sinh đi tham quan có trong khoảng từ 700 đến 800, trong đó có 300 học sinh khối 7. Tính số học sinh khối 6 đi tham quan.

Bài 6. (1 điểm)

Trong trò chơi bập bênh, mỗi em ngồi một đầu của thanh bập bênh AB dài 2m, có trung điểm M của đoạn thẳng AB được đặt trên một trụ để thanh bập bênh có thể lên xuống nhịp nhàng theo ý muốn của người chơi. Em hãy tính độ dài đoạn thẳng MA, MB.

Bài 7. (2 điểm) Trên tia Ox lấy hai điểm A và B sao cho OA = 5 cm, OB = 8 cm.

a) Chứng tỏ: điểm A nằm giữa hai điểm O, B và tính độ dài đoạn thẳng AB.

b) Trên tia Ox lấy điểm C sao cho OC = 2 cm. Chứng tỏ: điểm A là trung điểm của đoạn thẳng BC.

Read More

Toán thực tế (026)

Bác Bảy có một miếng đất hình chữ nhật kích thước 30 m và 50 m. Bác dự định làm một con đường hình bình hành băng ngang qua có kích thước như trong hình. Em hãy giúp bác Bảy tính diện tích con đường.

Xem đáp án

Read More

Toán thực tế (025)

Anh Bình góp vốn kinh doanh cùng một người bạn. Người bạn đó góp 150 triệu đồng, anh Bình góp 130 triệu đồng. Sau một thời gian họ được lãi 70 triệu đồng, tiền lãi được chia theo tỉ lệ góp vốn. Hãy tính tiền lãi mà anh Bình được nhận.

Xem đáp án

Read More

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2020$-$2021

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2020$-$2021

Bài 1. (1,5 điểm)
Cho parabol (P): $y = \dfrac{1}{4}x^2 $ và đường thẳng (d): $y = - \dfrac{1}{2}x + 2 $

a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2. (1,0 điểm)
Cho phương trình: $2x^2  - 5x - 3 = 0$ có 2 nghiệm là $x_1, x_2$.

Không giải phương trình, hãy tính giá trị của biểu thức $A = \left( {x_1  + 2x_2 } \right)\left( {x_2  + 2x_1 } \right)$.

Bài 3. (0,75 điểm)

Qui tắc sau đây cho ta biết CAN, CHI của năm X nào đó.

Để xác định CAN, ta tìm số dư $r$ trong phép chia X cho 10 và tra vào bảng 1.

Để xác định CHI, ta tìm số dư $s$ trong phép chia X cho 12 và tra vào bảng 2.

Ví dụ: năm 2020 có CAN là Canh, có CHI là Tí.

a) Em hãy sử dụng quy tắc trên để xác định CAN, CHI của năm 2005?

b) Bạn Hằng nhớ rằng Nguyễn Huệ lên ngôi hoàng đế, hiệu là Quang Trung vào năm Mậu Thân nhưng không nhớ rõ đó là năm bao nhiêu mà chỉ nhớ là sự kiện trên xãy ra vào cuối thế kỉ 18. Em hãy giúp Hằng xác định chính xác nam đó là năm bao nhiêu?

Bài 4. (0,75 điểm)

Cước điện thoại $y$ (nghìn đồng) là số tiền mà người sử dụng điện thoại cần trả hàng tháng, nó phụ thuộc vào lượng thời gian gọi $x$ (phút) của người đó trong tháng. Mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất $y = ax + b$. Hãy tìm $a$, $b$ biết rằng nhà bạn Nam trong tháng 5 đã gọi 100 phút với số tiền là 40 nghìn đồng và trong tháng 6 đã gọi 40 phút với số tiền là 28 nghìn đồng.

Bài 5. (1,0 điểm)

Theo quy định của cửa hàng xe máy, để hoàn thành chỉ tiêu trong một tháng, mỗi nhân viên phải bán được trung bình một chiếc xe máy một ngày. Nhân viên nào hoàn thành chỉ tiêu trong một tháng thì nhận được lương cơ bản là 8 000 000 đồng. Nếu trong tháng nhân viên nào bán vượt chỉ tiêu thì được thưởng thêm 8% tiền lời của số xe máy bán vượt chỉ tiêu đó. Trong tháng 5 (có 31 ngày), anh Thành nhận được số tiền là 9 800 000 đồng (bao gồm cả lương cơ bản và tiền thưởng thêm của tháng đó). Hỏi anh Thành đã bán được bao nhiêu chiếc xe máy trong tháng 5, biết rằng mỗi xe máy bán ra thì cửa hàng thu lời được 2 500 000 đồng.

Bài 6. (1,0 điểm)

Anh Minh vừa mới xây một cái hồ trữ nước cạnh nhà có hình dạng hộp chữ nhật kích thước 2m ´ 2m ´ 1m. Hiện hồ chưa có nước nên anh Minh phải ra sông lấy nước. Mỗi lần ra sông anh gánh được 1 đôi nước đầy gồm 2 thùng hình trụ bằng nhau có bán kính đáy 0,2 m, chiều cao 0,4 m.

a) Tính lượng nước ($m^3$) anh Minh đổ vào hồ sau mỗi lần gánh (ghi kết quả làm tròn đến 2 chữ số thập phân). Biết trong quá trình gánh nước về thì lượng nước bị hao hụt khoảng 10% và công thức tính thể tích hình trụ là $V = \pi R^2 h$.

b) Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy hồ? Bỏ qua thể tích thanh hồ.

Bài 7. (1,0 điểm)

Sau buổi sinh hoạt ngoại khóa, nhóm bạn của Thư rủ nhau đi an kem ở một quán gần trường. Do quán mới khai trương nên có khuyến mãi, bắt đầu từ ly thứ 5 giá mỗi ly kem được giảm 1 500 đồng so với giá ban đầu. Nhóm của Thư mua 9 ly kem với số tiền là 154 500 đồng. Hỏi giá của một ly kem ban đầu?

Bài 8. (3,0 điểm)

Cho đường tròn tâm $O$; bán kính $R$ và điểm $A$ nằm ngoài đường tròn sao cho $OA > 2R$. Từ $A$ kẻ 2 tiếp tuyến $AD$, $AE$ đến đường tròn ($O$) ($D$, $E$ là 2 tiếp điểm). Lấy điểm $M$ nằm trên cung nhỏ $DE$ sao cho $MD > ME$. Tiếp tuyến của đường tròn ($O$) tại $M$ cắt $AD$, $AE$ lần lượt tại $I$, $J$. Đường thẳng $DE$ cắt $OJ$ tại $F$.

a) Chứng minh: $OJ$ là đường trung trực của đoạn thẳng $ME$ và $\widehat{OMF} = \widehat{OEF}$.

b) Chứng minh: tứ giác $ODIM$ nội tiếp và 5 điểm $I$, $D$, $O$, $F$, $M$ cùng nằm trên một đường tròn.

c) Chứng minh: $\widehat{JOM} = \widehat{IOA}$ và $\sin \widehat{IOA} = \dfrac{{MF}}{{IO}}$.

Read More

ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2018$-$2019 QUẬN 11 TPHCM

ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2018$-$2019 QUẬN 11 TPHCM

Bài 1. (3 điểm) Thực hiện phép tính:

a) $\dfrac{5}{7} - \dfrac{6}{5}.\dfrac{{45}}{{42}}$

b) $\dfrac{{ - 1}}{5} + \dfrac{2}{{11}} + \dfrac{{ - 4}}{5} + \dfrac{9}{{11}} - 1\dfrac{1}{2}$

c) $\dfrac{{ - 5}}{7}.\dfrac{9}{{14}} + \dfrac{{ - 5}}{7}.\dfrac{5}{{14}} - \dfrac{2}{7}$

d) $75\%  - \left( {1,25 - 2\dfrac{3}{4}} \right):\dfrac{9}{2}$

Bài 2. (2,5 điểm) Tìm x, biết:

a) $x + \dfrac{1}{6} = \dfrac{{ - 4}}{3}$
b) $2x - \dfrac{1}{2} = \dfrac{{ - 1}}{3} + \dfrac{3}{4}$
c) $1,5 - \left( {\dfrac{3}{5}x + 70\% } \right) =  - 2\dfrac{1}{2}$

Bài 3. (2 điểm)

a) Bạn An đọc một quyển sách dày 120 trang trong 3 ngày. Ngày thứ nhất An đọc được $\dfrac{1}{3}$ số trang của quyển sách. Ngày thứ hai An đọc tiếp 40% số trang còn lại. Hỏi ngày thứ ba An đọc được bao nhiêu trang?

b) Lớp 6A có $\dfrac{7}{12}$ số học sinh thích học môn Toán, $\dfrac{5}{18}$ số học sinh thích học môn Ngữ văn và $\dfrac{1}{6}$ số học sinh thích học môn tiếng Anh. Hỏi môn nào được học sinh lớp 6A thích học nhiều nhất? Vì sao?

c) Nhân dịp kỷ niệm 44 năm ngày Giải phóng miền Nam, Thống nhất đất nước (30/04/1975 – 30/04/2019), nhà sách giảm 20% giá được ghi trên bìa các quyển sách. Một quyển sách có giá bìa là 80 000 đồng, hỏi người mua quyển sách đó phải trả bao nhiêu tiền?

Bài 4. (2 điểm) Trên cùng một nửa mặt phẳng có bờ chứa tia Ox, vẽ hai tia Oy và Oz sao cho $\widehat {xOy} = {30^0}$ và $\widehat {xOz} = {120^0}$.

a) Trong ba tia Ox, Oy, Oz thì tia nào nằm giữa hai tia còn lại? Tính số đo $\widehat {yOz}$.

b) Vẽ tia Ot là tia phân giác của $\widehat {yOz}$. Tính số đo $\widehat {xOt}$.

Bài 5. (0,5 điểm) Tính hợp lý:

$M = \dfrac{2}{7.9} + \dfrac{3}{{9.12}} + \dfrac{4}{{12.16}} + \dfrac{5}{{16.21}}$

Read More

[LATEX] Cách bật Pdf Viewer trong Texmaker & bước đầu tạo một tài liệu LaTex

Đây là video hướng dẫn các bạn bật Pdf Viewer trong Texmaker và bước đầu tạo một tài liệu Latex đơn giản.

Read More

Cách khắc phục lỗi chữ ngắt quãng trong Word

Đây là video hướng dẫn các bạn sửa lỗi chữ bị ngắt quãng, có khoảng trắng giữa các kí tự trong mỗi từ khi soạn thảo văn bản trong Word.

Read More

[ĐẠI SỐ 9] GIẢI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH

❄ GIẢI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH

Bước 1: Lập hệ phương trình.

_ Chọn hai ẩn và đặt điều kiện thích hợp cho chúng.

_ Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.

_ Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2: Giải hệ phương trình nói trên.

Bước 3: Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán đã cho và kết luận.

VD1: Một hình chữ nhật có chu vi bằng 140 m. Chiều dài hơn chiều rộng 10 m. Tính diện tích hình chữ nhật.

Giải. 

Gọi chiều dài hình chữ nhật là x, chiều rộng hình chữ nhật là y (mét; x, y > 0)
Theo đề bài, ta có hệ phương trình:

$\begin{cases}2(x + y) =140\\x - y = 10\end{cases}$
$ \Leftrightarrow $ $\begin{cases}x + y = 70\\x - y = 10\end{cases}$
$ \Leftrightarrow $ $\begin{cases}x = 40\\y = 30\end{cases}$
Vậy hình chữ nhật có chiều dài 40 m, chiều rộng 30 m.

VD2: Năm nay tuổi cha gấp 10 lần tuổi con. Sáu năm nữa tuổi cha gấp 4 lần tuổi con. Hỏi năm nay mỗi người bao nhiêu tuổi?

Giải. 

Gọi tuổi cha năm nay là x, tuổi con năm nay là y (x, y nguyên dương)
Theo đề bài, ta có hệ phương trình:

$\begin{cases}x = 10y\\x + 6 = 4(y + 6)\end{cases}$
...

$ \Leftrightarrow $ $\begin{cases}x = 30\\y = 3\end{cases}$
Vậy năm nay cha 30 tuổi, con 3 tuổi.

Bài tập Giải toán bằng cách lập hệ phương trình

Read More

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2019$-$2020

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2019$-$2020

Bài 1. (1,5 điểm)
Cho parabol (P): $y =  - \dfrac{1}{2}x^2 $ và đường thẳng (d): $y = x - 4$.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2. (1,0 điểm)
Cho phương trình: $2x^2  - 3x - 1 = 0$ có 2 nghiệm là $x_1, x_2$.

Không giải phương trình, hãy tính giá trị của biểu thức $A = \dfrac{{x_1  - 1}}{{x_2  + 1}} + \dfrac{{x_2  - 1}}{{x_1  + 1}}$

Bài 3. (0,75 điểm)

Qui tắc sau đây cho ta biết được ngày $n$, tháng $t$, năm 2019 là ngày thứ mấy trong tuần.
    Đầu tiên, ta tính giá trị của biểu thức $T = n + H$, ở đây $H$ được xác định bởi bảng sau:

     Sau đó, lấy $T$ chia cho 7 ta được số dư $r$ $\left( {0 \le r \le 6} \right)$.

      Nếu $r = 0$ thì ngày đó là ngày thứ Bảy.

      Nếu $r = 1$ thì ngày đó là ngày Chủ Nhật.

      Nếu $r = 2$ thì ngày đó là ngày thứ Hai.

      Nếu $r = 3$ thì ngày đó là ngày thứ Ba.

      …

      Nếu $r = 6$ thì ngày đó là ngày thứ Sáu.

Ví dụ:

+ Ngày 31/12/2019 có $n$ = 31; $t$ = 12; $H$ = 0 $\Rightarrow$ $T$ = 31 + 0 = 31; số 31 chia cho 7 có số dư là 3, nên ngày đó là thứ Ba.

a) Em hãy sử dụng quy tắc trên để xác định các ngày 02/9/2019 va 20/11/2019 là thứ mấy?

b) Bạn Hằng tổ chức sinh nhật của mình trong tháng 10/2019. Hỏi sinh nhật của bạn Hằng là ngày mấy? Biết rằng ngày sinh nhật của Hằng là một bội số của 3 và là thứ Hai.

Bài 4. (0,75 điểm)

Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất y (atm) và độ sâu x (m) dưới mặt nước là một hàm số bậc nhất có dạng y = a + b.

a) Xác định các hệ số a và b.

b) Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất là 2,85 atm?

Bài 5. (1,0 điểm)

Một nhóm gồm 31 bạn học sinh tổ chức một chuyến đi du lịch (chi phí chuyến đi được chia đều cho mỗi bạn tham gia). Sau khi đã hợp đồng xong, vào giờ chót có 3 bạn bận việc đột xuất không đi được nên họ không đóng tiền. Cả nhóm thống nhất mỗi bạn còn lại sẽ đóng thêm 18000 đồng so với dự kiến ban đầu để bù lại cho 3 bạn không tham gia. Hỏi tổng chi phí chuyến đi là bao nhiêu?

Bài 6. (1,0 điểm)

Cuối năm học, các bạn lớp 9A chia làm hai nhóm, mỗi nhóm chọn một khu vườn sinh thái ở Bắc bán cầu để tham quan. Khi mở hệ thống định vị GPS, họ phát hiện một sự trùng hợp khá thú vị là hai vị trí mà hai nhóm chọn đều nằm trên cùng một kinh tuyến và lần lượt ở các vĩ tuyến 47$^o$ và 72$^o$.

a) Tính khoảng cách (làm tròn đến hàng trăm) giữa hai vị trí đó, biết rằng kinh tuyến là một cung tròn nối liền hai cực của trái đất và có độ dài khoảng 20000 km.

b) Tính (làm tròn đến hàng trăm) độ dài bán kính và đường xích đao của trái đất. Từ kết quả của bán kính (đã làm tròn), hãy tính thể tích của trái đất, biết rằng trái đất có dạng hình cầu và thể tích của hình cầu được tính theo công thức $V = \dfrac{4}{3}.3,14.R^3 $ với $R$ là bán kính hình cầu.

Bài 7. (1,0 điểm)

Bạn Dũng trung bình tiêu thụ 15 ca-lo cho mỗi phút bơi và 10 ca-lo cho mỗi phút chạy bộ. Hôm nay, Dũng mất 1,5 giờ cho cả hai hoạt động trên và tiêu thụ hết 1200 ca-lo. Hỏi hôm nay, bạn Dũng mất bao nhiêu thời gian cho mỗi hoạt động?

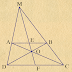
Bài 8. (3,0 điểm) Cho tam giác nhọn $ABC$ ($AB < AC$) nội tiếp đường tròn ($O$). Hai đường cao $BD$ và $CE$ của tam giác $ABC$ cắt nhau tại $H$. Đường thẳng $AH$ cắt $BC$ và ($O$) lần lượt tại $F$ và $K$ (K $\ne$ A). Gọi $L$ là hình chiếu của $D$ lên $AB$.

a) Chứng minh rằng tứ giác $BEDC$ nội tiếp và $BD^2  = BL.BA$.

b) Gọi $J$ là giao điểm của $KD$ và ($O$) (J $\ne$ K). Chứng minh $\widehat{BJK} = \widehat{BDE}$.

c) Gọi $I$ là giao điểm của $BJ$ và $ED$. Chứng minh tứ giác $ALIJ$ nội tiếp và $I$ là trung điểm của $ED$.

Read More

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2018$-$2019

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2018$-$2019

Bài 1. (1,5 điểm)
Cho parabol (P): $y = x^2 $ và đường thẳng (d): $y = 3x - 2$.
a) Vẽ (P) và (d) trên cùng hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép tính.

Bài 2. (1,0 điểm)
Cho phương trình: $3x^2  - x - 1 = 0$ có 2 nghiệm là $x_1, x_2$.

Không giải phương trình, hãy tính giá trị của biểu thức $A = x_1^2  + x_2^2 $

Bài 3. (0,75 điểm)

Mối quan hệ giữa thang nhiệt độ F (Fahrenheit) và thang nhiệt độ C (Celsius) được cho bởi công thức $T_F  = 1,8.T_C  + 32$ trong đó $T_C$ là nhiệt độ tính theo độ C và $T_F$ là nhiệt độ tính theo độ F. Ví dụ $T_C  = 0^o C$ tương ứng với $T_F  = 32^o F$.
a) Hỏi $25^o C$ tương ứng với bao nhiêu độ F?
b) Các nhà khoa học đã tìm ra mối liên hệ giữa A là số tiếng kêu của một con dế trong một phút và $T_F$ là nhiệt độ cơ thể của nó bởi công thức: $A = 5,6.T_F  - 275$, trong đó nhiệt độ $T_F$ tính theo độ F. Hỏi nếu con dế kêu 106 tiếng trong một phút thì nhiệt độ của nó khoảng bao nhiêu độ C? (làm tròn đến hàng đơn vị)

Bài 4. (0,75 điểm)
Kim tự tháp Kheops – Ai Cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214 m cạnh đáy của nó dài 230 m.
a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến chữ số thập phân thứ nhất).
b) Cho biết thể tích của hình chóp được tính theo công thức $V = \dfrac{1}{3}S.h$, trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo $m^3$ thể tích của kim tự tháp này (làm tròn đến hàng nghìn).

Bài 5. (1,0 điểm)

Siêu thị A thực hiện chương trình giảm giá cho khách hàng mua loại túi bột giặt 4 kg như sau: Nếu mua 1 túi thì được giảm 10 000 đồng so với giá niêm yết. Nếu mua 2 túi thì túi thứ nhất được giảm 10 000 đồng và túi thứ hai được giảm 20 000 đồng so với giá niêm yết. Nếu mua từ 3 túi trở lên thì ngoài 2 túi đầu được hưởng chương trình giảm giá như trên, từ túi thứ ba trở đi mỗi túi sẽ được giảm 20% so với giá niêm yết.

a) Bà Tư mua 5 túi bột giặt loại 4 kg ở siêu thị A thì phải trả số tiền là bao nhiêu, biết rằng loại túi bột giặt mà bà Tư mua có giá niêm yết là 150 000 đồng/túi.

b) Siêu thị B lại có hình thức giảm giá khác cho loại túi bột giặt nêu trên là: nếu mua từ 3 túi trở lên thì sẽ giảm giá 15% cho mỗi túi. Nếu bà Tư mua 5 túi bột giặt thì bà Tư nên mua ở siêu thị nào để số tiền phải trả là ít hơn? Biết rằng giá niêm yết của hai siêu thị là như nhau.

Bài 6. (1,0 điểm)

Nhiệt độ sôi của nước không phải lúc nào cũng là 100$^o$C mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn Thành phố Hồ Chí Minh có độ cao xem như ngang mực nước biển (x = 0 m) thì nước có độ sôi y = 100$^o$C nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao x = 3600 m so với mực nước biển thì nhiệt độ sôi của nước là y = 87$^o$C. Ở độ cao trong khoảng vài km, người ta thấy mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất $y=ax+b$ có đồ thị như sau: 

a) Xác định các hệ số a và b.

b) Thành phố Đà Lạt có độ cao 1500 m so với mực nước biển. Hỏi nhiệt độ sôi của nước ở thành phố này là bao nhiêu?

Bài 7. (1,0 điểm)

Năm học 2017 – 2018, Trường THCS Tiến Thành có ba lớp 9 gồm 9A, 9B, 9C trong đó lớp 9A có 35 học sinh và lớp 9B có 40 học sinh. Tổng kết cuối năm học, lớp 9A có 15 học sinh đạt danh hiệu học sinh giỏi, lớp 9B có 12 học sinh đạt danh hiệu học sinh giỏi, lớp 9C có 20% học sinh đạt danh hiệu học sinh giỏi và toàn khối lớp 9 có 30% học sinh đạt danh hiệu học sinh giỏi. Hỏi lớp 9C có bao nhiêu học sinh?

Bài 8. (3,0 điểm) Cho tam giác nhọn ABC có BC = 8cm. Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và D. Hai đường thẳng BD và CE cắt nhau tại H.
a) Chứng minh: AH vuông góc với BC.
b) Gọi K là trung điểm của AH. Chứng minh tứ giác OEKD nội tiếp.
c) Cho $\widehat{BAC} = 60^0 $. Tính độ dài đoạn DE và tỉ số diện tích của hai tam giác AED và ABC.

Read More

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2017$-$2018

ĐỀ THI TUYỂN SINH LỚP 10 THPT TPHCM NĂM HỌC 2017$-$2018

Bài 1. Giải các phương trình và hệ phương trình sau:

a) Giải phương trình: $x^2  = \left( {x - 1} \right)\left( {3x - 2} \right)$

b) Một miếng đất hình chữ nhật có chu vi 100m. Tính chiều dài và chiều rộng của miếng đất, biết rằng 5 lần chiều rộng hơn 2 lần chiều dài 40m.

Bài 2.

Trong mặt phẳng tọa độ Oxy:
a) Vẽ đồ thị (P) của hàm số $y = \dfrac{1}{4}x^2 $.

b) Cho đường thẳng (D): $y = \dfrac{3}{2}x + m$ đi qua điểm C(6; 7). Tìm tọa độ giao điểm của (D) và (P).

Bài 3.

1) Thu gọn biểu thức sau: $A = \left( {\sqrt 3  + 1} \right)\sqrt {\dfrac{{14 - 6\sqrt 3 }}{{5 + \sqrt 3 }}} $

2) Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng AB dài 762m, $\widehat A = 6^0 $,  $\widehat B = 4^0 $.

a) Tính chiều cao h của con dốc.

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ trung bình xuống dốc là 19 km/h.

Bài 4. Cho phương trình: $x^2  - \left( {2m - 1} \right)x + m^2  - 1 = 0$ (1) (x là ẩn số)

a) Tìm điều kiện của m để phương trình (1) có hai nghiệm phân biệt.

b) Định m để hai nghiệm $x_1$, $x_2$ của phương trình (1) thỏa mãn:

$\left( {x_1  - x_2 } \right)^2  = x_1  - 3x_2 $

Bài 5. Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt các đoạn BC và OC lần lượt tại D và I. Gọi H là hình chiếu của A lên OC; AH cắt BC tại M.

a) Chứng minh: Tứ giác ACDH nội tiếp và $\widehat {CHD} = \widehat {ABC}$.

b) Chứng minh: Hai tam giác OHB và OBC đồng dạng với nhau và HM là tia phân giác của góc BHD.

c) Gọi K là trung điểm của BD. Chứng minh: MD.BC = MB.CD và MB.MD = MK.MC.

d) Gọi E là giao điểm của AM và OK; J là giao điểm của IM và (O) (J khác I). Chứng minh: Hai đường thẳng OC và EJ cắt nhau tại một điểm nằm trên (O).

Read More