Sunday, December 23, 2018
On 6:56 PM by MATH CHANNEL in Đề thi Toán 9 2 comments
HKI
ĐỀ THI TOÁN 9 HỌC KÌ I NĂM HỌC 2018$-$2019 QUẬN 11 TPHCM
HKII
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2015$-$2016 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2014$-$2015 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2012$-$2013 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2011$-$2012 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2009$-$2010 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2008$-$2009 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ I NĂM HỌC 2018$-$2019 QUẬN 11 TPHCM
HKII
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2015$-$2016 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2012$-$2013 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2009$-$2010 QUẬN 11 TPHCM
ĐỀ THI TOÁN 9 HỌC KÌ II NĂM HỌC 2008$-$2009 QUẬN 11 TPHCM
On 6:48 PM by MATH CHANNEL in Đề thi Toán 9 1 comment
ĐỀ THI TOÁN 9 HỌC KÌ I NĂM HỌC 2018$-$2019 QUẬN 11 TPHCM
Bài 1. (2 điểm) Thực hiện phép tính:
Bài 1. (2 điểm) Thực hiện phép tính:
a) $A = 3\sqrt2 - 2\sqrt8 + \sqrt{50}$
b) $B = \sqrt {\left( {5 + \sqrt 3 } \right)^2 } + \sqrt {\left( {2 - \sqrt 3 } \right)^2 }$
b) $B = \sqrt {\left( {5 + \sqrt 3 } \right)^2 } + \sqrt {\left( {2 - \sqrt 3 } \right)^2 }$
Bài 2. (2 điểm) Trên mặt phẳng tọa độ Oxy cho đường thẳng (d1): $y = 2x - 3$
a) (d1).
b) Tìm tọa độ giao điểm A của (d1) và
(d2): $y = - \dfrac{1}{2}x + 2$ bằng phép toán.
Bài 3. (1 điểm) Giá bán một máy tính được giảm 10%. Nếu mua
online thì được giảm tiếp 5% trên giá đã giảm. Hỏi khi mua online thì ta phải
trả bao nhiêu tiền (giao hàng miễn phí)? Biết giá máy tính là 15 triệu đồng (đã
bao gồm VAT).
Bài 4. (1 điểm) Một người đứng cách chân tòa nhà BITEXCO (Thành phố Hồ Chí Minh) một khoảng BC = 151,5m nhìn thấy đỉnh tòa nhà này theo góc nghiêng $\widehat{BCA} = 60^0 $). Tính chiều cao AB của tòa nhà. (Học sinh vẽ sơ đồ vào bài làm và làm tròn kết quả đến hàng đơn vị)
Bài 4. (1 điểm) Một người đứng cách chân tòa nhà BITEXCO (Thành phố Hồ Chí Minh) một khoảng BC = 151,5m nhìn thấy đỉnh tòa nhà này theo góc nghiêng $\widehat{BCA} = 60^0 $). Tính chiều cao AB của tòa nhà. (Học sinh vẽ sơ đồ vào bài làm và làm tròn kết quả đến hàng đơn vị)
Bài 5. (1 điểm) Ông A muốn pha chế nhớt và xăng theo một tỷ lệ
phù hợp khoảng chừng 1 : 25 để chạy máy cưa. Ông có một bình chứa 1 lít trong đó
tỷ lệ nhớt với xăng là 1 : 11 và một bình chứa 2 lít trong đó tỉ lệ nhớt với xăng
là 1 : 99 mỗi lít. Ông trộn cả hai bình vào một bình 3 lít. Hỏi tỷ lệ nhớt và xăng
đã phù hợp chưa?
Bài 6. (3 điểm) Từ
một điểm A ngoài (O; R) với OA > 2R, vẽ hai tiếp tuyến AB, AC (B, C là hai
tiếp điểm).
a)
Chứng minh: $\Delta$OAB và $\Delta$OAC vuông, suy ra 4 điểm A, B, O, C cùng
thuộc một đường tròn.
b)
Vẽ BI $\bot$ AC tại I (I $\in$ AC), CK $\bot$ AB tại
K (K $\in$ AB ), BI cắt CK tại M. Chứng minh: OA BC
Sunday, July 29, 2018
On 11:32 PM by MATH CHANNEL in Math Puzzles 2 comments
Tuesday, July 24, 2018
Sunday, July 1, 2018
On 9:37 PM by MATH CHANNEL in Đại số 9 2 comments
Tuesday, June 19, 2018
On 6:25 AM by MATH CHANNEL in Đại số 9 2 comments
Monday, June 18, 2018
On 6:55 PM by MATH CHANNEL in Toán thực tế 3 comments
Ta có thể xem kim phút và kim giờ của đồng hồ là
hai tia chung gốc (gốc trùng với trục quay của hai kim). Tại mỗi thời điểm hai
kim tạo thành một góc. Em hãy tìm số đo của góc tạo bởi kim phút và kim giờ của
đồng hồ vào lúc 2 giờ 30 phút.
Xem đáp án
Xem đáp án
Sunday, June 17, 2018
Thursday, June 14, 2018
On 6:27 AM by MATH CHANNEL in Đề thi Toán 6 3 comments
ĐỀ THI TOÁN 6 HỌC KÌ II NĂM HỌC 2017$-$2018 QUẬN 11 TPHCM
Bài 1. (3 điểm) Thực hiện phép tính:
Bài 1. (3 điểm) Thực hiện phép tính:
a) $\dfrac{2}{3} - \dfrac{5}{6} + \dfrac{3}{4}$
b) $\dfrac{{14}}{{21}} + \dfrac{{ - 8}}{5} + \dfrac{7}{{21}} + \dfrac{3}{5}$c) $\dfrac{{11}}{{19}}.\dfrac{{ - 12}}{{17}} + \dfrac{{11}}{{19}}.\dfrac{{ - 5}}{{17}} + 2$
d) $\dfrac{2}{{15}} - 1,6:\left( {75\% + 5\dfrac{1}{4}} \right)$
Bài 2. (2,5 điểm) Tìm x, biết:
a) $x + \dfrac{5}{8} = \dfrac{{ - 3}}{4}$
b) $\dfrac{x}{{ - 3}} = \dfrac{8}{6}$
c) $4 - \left( {\dfrac{1}{2}x + \dfrac{3}{4}} \right) = - 1,5$
b) $\dfrac{x}{{ - 3}} = \dfrac{8}{6}$
c) $4 - \left( {\dfrac{1}{2}x + \dfrac{3}{4}} \right) = - 1,5$
Bài 3. (1,5 điểm)
a)
b)
Bài 4. (2,5 điểm) Trên cùng một nửa mặt phẳng có bờ chứa tia Oa, vẽ hai tia Ob và Oc sao cho $\widehat {aOb} = {70^0}$ và $\widehat {aOc} = {120^0}$.
a) Trong ba tia Oa, Ob, Oc thì tia nào nằm giữa hai tia còn lại? Vì sao?
b) Tính số đo $\widehat {bOc}$.
c) Vẽ tia Ot là tia đối của tia Ob, tia Om là tia phân giác của $\widehat {cOt}$. Tính số đo $\widehat {mOb}$.
Bài 5. (0,5 điểm) Tính hợp lý:
$M = \dfrac{1}{5} + \dfrac{1}{{20}} + \dfrac{1}{{44}} + \dfrac{1}{{77}} + \dfrac{1}{{119}} + \dfrac{1}{{170}}$Tuesday, June 12, 2018
Tuesday, June 5, 2018
Monday, June 4, 2018
Thursday, May 31, 2018
On 11:31 PM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán 1:}}$ Lúc 7 giờ, một ca nô xuôi dòng từ bến A đến bến
B cách nhau 36km rồi quay trở về bến A lúc 11 giờ 30 phút. Tính vận tốc của ca
nô biết vận tốc dòng nước là 6km/h.
$\boxed{\text {Bài toán 2:}}$ Khoảng cách giữa hai bến sông A và B là 30km. Một chiếc thuyền máy xuôi dòng từ A đến B rồi từ B ngược dòng trở về A ngay. Cả đi và về, thuyền máy mất 5 giờ 20 phút. Tính vận tốc của dòng nước, cho biết vận tốc thực của thuyền máy là 12km/h.
$\boxed{\text {Bài toán 3:}}$ Một công nhân phải hoàn thành 50 sản phẩm trong một thời gian qui định. Do tăng năng suất mỗi giờ 5 sản phẩm nên hoàn thành sớm hơn dự định 1 giờ 40 phút. Hỏi mỗi giờ người công nhân dự định làm được bao nhiêu sản phẩm?
$\boxed{\text {Bài toán 4:}}$ Theo kế hoạch, một xưởng may phải may xong 280 bộ quần áo trong một thời gian qui định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 5 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế, xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may xong bao nhiêu bộ quần áo?
$\boxed{\text {Bài toán 5:}}$ Một đoàn tàu đánh cá dự định đánh bắt 1800 tấn cá trong một số ngày nhất định. Do bị bão nên trong 3 ngày đầu tiên đoàn đánh bắt ít hơn kế hoạch 20 tấn mỗi ngày. Trong các ngày còn lại, đoàn đánh bắt vượt hơn kế hoạch 20 tấn mỗi ngày. Vì vậy đoàn đã hoàn thành kế hoạch đánh bắt trước thời hạn 2 ngày. Hỏi theo kế hoạch mỗi ngày đoàn tàu đánh bắt bao nhiêu tấn cá và thời gian đánh bắt theo kế hoạch là bao nhiêu ngày?
$\boxed{\text {Bài toán 2:}}$ Khoảng cách giữa hai bến sông A và B là 30km. Một chiếc thuyền máy xuôi dòng từ A đến B rồi từ B ngược dòng trở về A ngay. Cả đi và về, thuyền máy mất 5 giờ 20 phút. Tính vận tốc của dòng nước, cho biết vận tốc thực của thuyền máy là 12km/h.
$\boxed{\text {Bài toán 3:}}$ Một công nhân phải hoàn thành 50 sản phẩm trong một thời gian qui định. Do tăng năng suất mỗi giờ 5 sản phẩm nên hoàn thành sớm hơn dự định 1 giờ 40 phút. Hỏi mỗi giờ người công nhân dự định làm được bao nhiêu sản phẩm?
$\boxed{\text {Bài toán 4:}}$ Theo kế hoạch, một xưởng may phải may xong 280 bộ quần áo trong một thời gian qui định. Đến khi thực hiện, mỗi ngày xưởng đã may được nhiều hơn 5 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế, xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may xong bao nhiêu bộ quần áo?
$\boxed{\text {Bài toán 5:}}$ Một đoàn tàu đánh cá dự định đánh bắt 1800 tấn cá trong một số ngày nhất định. Do bị bão nên trong 3 ngày đầu tiên đoàn đánh bắt ít hơn kế hoạch 20 tấn mỗi ngày. Trong các ngày còn lại, đoàn đánh bắt vượt hơn kế hoạch 20 tấn mỗi ngày. Vì vậy đoàn đã hoàn thành kế hoạch đánh bắt trước thời hạn 2 ngày. Hỏi theo kế hoạch mỗi ngày đoàn tàu đánh bắt bao nhiêu tấn cá và thời gian đánh bắt theo kế hoạch là bao nhiêu ngày?
Wednesday, May 30, 2018
On 11:21 PM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán:}}$ Cho phương trình: ${x^2} - 2mx + 2m - 2 = 0$ ($x$ là ẩn số)
a) Chứng minh phương trình luôn có hai nghiệm phân biệt $x_1$ và $x_2$ với mọi giá trị của $m$.
b) Tìm giá trị lớn nhất của biểu thức $A = \dfrac{{6\left( {{x_1} + {x_2}} \right)}}{{x_1^2 + x_2^2 + 4\left( {{x_1} + {x_2}} \right)}}$
Monday, May 28, 2018
On 7:51 AM by MATH CHANNEL in Toán thực tế 2 comments
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (như hình vẽ bên dưới). Cho biết đoạn thẳng AB dài 762m, $\widehat A = {6^0}$, $\widehat B = {4^0}$.
a) Tính chiều
cao h của con dốc.
b) Hỏi bạn An đến
trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ
trung bình xuống dốc là 19 km/h.
Sunday, May 27, 2018
On 9:35 PM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán:}}$ Cho phương trình: ${x^2} - 2mx - 3{m^2} + 2m - 1 = 0$ ($x$ là ẩn số)
a) Chứng tỏ phương
trình luôn có hai nghiệm phân biệt $x_1$ và $x_2$ với mọi giá trị của $m$.
b) Tìm giá trị của $m$ để biểu thức $A = \dfrac{{ - 5}}{{x_1^2 + x_2^2 + 3{x_1}{x_2} + 4}}$ đạt giá trị nhỏ nhất.
Saturday, May 26, 2018
On 1:27 AM by MATH CHANNEL in Đại số 9 2 comments
Friday, May 25, 2018
On 4:10 AM by MATH CHANNEL in Đố Toán 2 comments
Hai người bộ hành nghỉ chân bên vệ đường, giở gói bánh bao ra ăn. Một người có năm chiếc, một người có ba chiếc. Họ cắt tàu lá chuối trải lên bãi cỏ, bỏ chung bánh vào cùng ăn. Bỗng có một người lái buôn vừa đi tới. Hai người mời người lái buôn cùng ăn với mình. Đang đói và thấy hai người mời niềm nở, khách không từ chối.
Ba người cùng lần lượt ăn hết tám cái bánh. Cứ mỗi cái bánh được bẻ ra ba phần. Họ ăn xong cái này lại cắt tiếp cái khác.
Ăn xong, người lái buôn vội đi, xin gởi lại tám đồng bạc.
Hai người có bánh đem tiền ra chia. Người có năm cái bánh nhất quyết phải lấy năm đồng. Người có ba chiếc bánh đòi phải chia đôi số tiền.
Hai người cãi nhau, bất phân thắng bại, đành đưa nhau đến cho quan sở tại phân xử.
Nếu bạn là quan sở tại thì bạn sẽ phân xử như thế nào?
Nếu bạn là quan sở tại thì bạn sẽ phân xử như thế nào?
| Số miếng (khi chia mỗi cái bánh ra 3 miếng bánh) |
Đã ăn | Còn dư | Số tiền nhận được tương ứng |
|
| Người có 3 cái bánh | 9 miếng | 8 miếng | 1 miếng | 1 đồng |
| Người có 5 cái bánh | 15 miếng | 8 miếng | 7 miếng | 7 đồng |
Sunday, May 20, 2018
Thursday, May 17, 2018
On 10:11 PM by MATH CHANNEL in Đại số 9 2 comments
Tuesday, May 15, 2018
On 11:28 PM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán:}}$ Cho phương trình: ${x^2} - \left( {3m - 2} \right)x - 3m = 0$ ($x$ là ẩn số)
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của $m$.
b) Gọi $x_1$, $x_2$ là hai nghiệm của phương trình. Tìm $m$ để biểu thức $A = x_1^2{x_2} + x_2^2{x_1}$ đạt giá trị lớn nhất.
Monday, May 14, 2018
On 9:49 PM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán:}}$ Cho phương trình: ${x^2} - \left( {m + 1} \right)x + m - 2 = 0$ ($x$ là ẩn số)
a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của $m$.
b) Gọi $x_1$, $x_2$ là hai nghiệm của phương trình. Tìm $m$ để biểu thức $A = x_1^2 + x_2^2 - 6{x_1}{x_2}$ đạt giá trị nhỏ nhất.
Sunday, May 13, 2018
Saturday, May 12, 2018
On 7:50 PM by MATH CHANNEL in Đại số 9 2 comments
Thursday, May 10, 2018
On 8:01 AM by MATH CHANNEL in Đại số 9 2 comments
Wednesday, May 9, 2018
On 5:59 AM by MATH CHANNEL in Đại số 9 2 comments
Tuesday, May 8, 2018
On 3:50 AM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán:}}$ Cho phương trình: ${x^2} - \left( {m - 3} \right)x + m - 5 = 0$ ($x$ là ẩn số)
a) Chứng minh: phương trình luôn có hai nghiệm phân biệt
với mọi giá trị của $m$.
b) Tìm $m$ để phương trình trên có hai nghiệm $x_1$, $x_2$ thỏa điều kiện:
$x_1^2 - 4{x_1} + x_2^2 - 4{x_2} = 11$
Sunday, May 6, 2018
On 12:51 AM by MATH CHANNEL in Đại số 9 2 comments
Friday, May 4, 2018
On 6:51 PM by MATH CHANNEL in Đại số 9 2 comments
$\boxed{\text {Bài toán:}}$ Cho phương trình: $3{x^2} - 6x - 4 = 0$ có hai nghiệm $x_1$, $x_2$. Tính giá trị của các biểu thức sau:

1) $\left| {{x_1} - {x_2}} \right|$
2) $x_1^2 + x_2^2$
3) $x_1^3 + x_2^3$
4) $x_1^4 + x_2^4$
5) $x_1^2 + x_2^2 - {x_1} - {x_2} + 5{x_1}{x_2}$
6) $\left( {3{x_1} - {x_2}} \right)\left( {3{x_2} - {x_1}} \right)$
7) $\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}}$
2) $x_1^2 + x_2^2$
3) $x_1^3 + x_2^3$
4) $x_1^4 + x_2^4$
5) $x_1^2 + x_2^2 - {x_1} - {x_2} + 5{x_1}{x_2}$
6) $\left( {3{x_1} - {x_2}} \right)\left( {3{x_2} - {x_1}} \right)$
7) $\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}}$
8) $\dfrac{1}{{{x_1} - 1}} + \dfrac{1}{{{x_2} - 1}}$
9) $\dfrac{{2x_2^2}}{{{x_1} + {x_2}}} + 2{x_1}$
10) $\dfrac{{3x_1^2 - 6{x_1}}}{{{x_2}}} + \dfrac{{3x_2^2 - 6{x_2}}}{{{x_1}}}$
Xem đáp án
9) $\dfrac{{2x_2^2}}{{{x_1} + {x_2}}} + 2{x_1}$
10) $\dfrac{{3x_1^2 - 6{x_1}}}{{{x_2}}} + \dfrac{{3x_2^2 - 6{x_2}}}{{{x_1}}}$
Xem đáp án
Wednesday, April 25, 2018
On 4:20 AM by MATH CHANNEL in Đại số 8 3 comments
❄ GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
Bước 1. Lập phương trình
_ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
_ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
_ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình
Bước 3. Kết luận
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
_ Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
_ Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
_ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình
Bước 3. Kết luận
Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
Tuesday, April 24, 2018
Monday, April 23, 2018
On 9:26 PM by MATH CHANNEL in Toán thực tế 2 comments
Một bạn vào cửa hàng mua một số bút chì và bút
bi. Giá mỗi cây bút chì là 15000 đồng và giá mỗi cây bút bi là 3000 đồng. Bạn đó
phải trả tổng cộng 45000 đồng. Hỏi bạn đó đã mua bao nhiêu cây bút chì và bao
nhiêu cây bút bi? Biết rằng số bút mỗi loại lớn hơn 1.
Friday, April 20, 2018
On 4:32 AM by MATH CHANNEL in Toán thực tế 2 comments
Theo quyết định Bộ Công Thương ban hành, giá bán
lẻ điện sinh hoạt từ 16/3 sẽ dao động trong khoảng từ 1484 đến 2587 đồng mỗi
kWh tùy bậc thang. Dưới đây là bảng so sánh biểu giá điện trước và sau khi điều
chỉnh:
a)
Nếu hộ A trung bình mỗi tháng tiêu thụ 120kWh thì theo giá mới số tiền phải trả
tăng lên bao nhiêu trong một tháng?
b)
Hộ B trong tháng 2 đã trả tiền sử dụng điện là 194170 đồng. Hỏi lượng điện mà hộ
B tiêu thụ trong tháng 2 là bao nhiêu?
c) Giả sử hộ C trong nửa tháng đầu được tính theo giá
cũ, trong nửa tháng sau được tính theo giá mới với mức sử dụng thực tế (bao gồm
nửa tháng đầu) và lượng điện tiêu thụ ở mỗi nửa tháng là bằng nhau. Số tiền cuối
tháng hộ C phải trả là 116350 đồng. Hỏi lượng điện mà hộ C tiêu thụ trong tháng
là bao nhiêu? Biết rằng lượng điệu tiêu thụ không vượt quá 100kWh.
a) Số tiền hộ A phải trả theo giá cũ: $50.1388 + 50.1433 + 20.1660 = 174250$ (đồng).
Số tiền hộ A phải trả theo giá mới: $50.1484 + 50.1533 + 20.1786 = 186570$ (đồng).
Số tiền tăng lên: $186570 - 174250 = 12320$ (đồng).
b) $50.1388 + 50.1433 = 141050$,
$50.1388 + 50.1433 + 100.1660 = 307050$.
Do $141050$ < $194170$ < $307050$ nên hộ B tiêu thụ từ $101$ đến $200$kWh.
Lượng điện mà hộ B tiêu thụ: $\left( {194170 - 141050} \right):1660 + 100 = 132$ kWh.
c) Gọi $x$ (kWh) là lượng điện mà hộ C tiêu thụ trong nửa tháng đầu với $x \le 50$
$\Rightarrow$ Lượng điện tiêu thụ trong tháng là $2x$.
Nếu $2x \le 50$ thì ta có phương trình: $x.1388 + x.1484 = 116350$, suy ra $x \approx 40,5$ (loại)
Nếu $2x > 50$ thì ta có phương trình: $x.1388 + \left( {50 - x} \right).1484 + \left( {2x - 50} \right).1533 = 116350$, suy ra $x = 40$.
Vậy lượng điện mà hộ C tiêu thụ trong tháng là $80$kWh.
Số tiền hộ A phải trả theo giá mới: $50.1484 + 50.1533 + 20.1786 = 186570$ (đồng).
Số tiền tăng lên: $186570 - 174250 = 12320$ (đồng).
b) $50.1388 + 50.1433 = 141050$,
$50.1388 + 50.1433 + 100.1660 = 307050$.
Do $141050$ < $194170$ < $307050$ nên hộ B tiêu thụ từ $101$ đến $200$kWh.
Lượng điện mà hộ B tiêu thụ: $\left( {194170 - 141050} \right):1660 + 100 = 132$ kWh.
c) Gọi $x$ (kWh) là lượng điện mà hộ C tiêu thụ trong nửa tháng đầu với $x \le 50$
$\Rightarrow$ Lượng điện tiêu thụ trong tháng là $2x$.
Nếu $2x \le 50$ thì ta có phương trình: $x.1388 + x.1484 = 116350$, suy ra $x \approx 40,5$ (loại)
Nếu $2x > 50$ thì ta có phương trình: $x.1388 + \left( {50 - x} \right).1484 + \left( {2x - 50} \right).1533 = 116350$, suy ra $x = 40$.
Vậy lượng điện mà hộ C tiêu thụ trong tháng là $80$kWh.
Thursday, April 19, 2018
On 6:39 AM by MATH CHANNEL in Toán thực tế 3 comments
Hai ngư dân đứng ở một bên bờ sông cách nhau
250m cùng nhìn thấy một cù lao trên sông với các góc nâng lần lượt là 30$^0$ và 40$^0$. Tính khoảng cách d từ bờ sông đến cù lao.
Subscribe to:
Comments (Atom)
Search
Popular Posts
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Hình thang cân 1. Hình thang có hai góc kề một đáy bằng nhau là hìn...
-
$\boxed{\text {Bổ đề hình thang: }}$ Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điể...
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TAM GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Tam giác cân 1. Tam giác có hai cạnh bằng nhau là tam giác cân....
-
$\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ ABC. Chứng minh rằng...
-
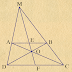
$\boxed{\text {Bài toán 1: }}$ (Đề thi HKII 2008-2009 Q11 TpHCM) Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF c...
-
Để tìm ƯCLN, BCNN của các số tự nhiên, người ta thường dùng những cách sau: Cách 1 : Phân tích các số ra thừa số nguyên tố Vd: Tìm ƯC...
-
Bạn cần download tài liệu, ebook,... phục vụ cho việc học tập nghiên cứu từ các trang Scribd, Issuu, Slideshare và Academia một cách nhanh...
-
Chương trình Tìm Ước chung lớn nhất và Bội chung nhỏ nhất của một dãy các số tự nhiên import java.util.Scanner; public class Main ...
-
Dãy số Fibonacci được định nghĩa như sau: F[0] =1, F[1] = 1; F[n] = F[n-1] + F[n-2] với n>=2. Hãy viết chương trình tìm số Fibonacci thứ ...
-
Chương trình Chuyển đổi một số tự nhiên ở hệ thập phân thành số ở hệ nhị phân, bát phân, thập lục phân và hệ cơ số bất kì import java.u...
Recent Posts
Categories
- Công nghệ thông tin
- Đại số 10
- Đại số 7
- Đại số 8
- Đại số 9
- Đề thi Toán 6
- Đề thi Toán 7
- Đề thi Toán 8
- Đề thi Toán 9
- Đố Toán
- Grade 6 Math
- Grade 8 Math
- Grade 9 Math
- Hình học 6
- Hình học 7
- Hình học 8
- Hình học 9
- Khác
- Lập trình Java cơ bản
- Math Puzzles
- Mathematical game
- Phương pháp học Toán
- Số học 6
- Số và Đại số 6
- Toán tham khảo 6
- Toán tham khảo 8
- Toán tham khảo 9
- Toán thực tế
- Toán và cuộc sống
Blog Archive
-
▼
2018
(48)
-
►
May
(17)
- [ĐẠI SỐ 9] BÀI TẬP GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG ...
- BÀI TẬP ĐỊNH LÍ VIÈTE (12)
- Toán thực tế (020)
- BÀI TẬP ĐỊNH LÍ VIÈTE (11)
- BÀI TẬP ĐỊNH LÍ VIÈTE (10)
- Câu đố Toán học (002)
- Câu đố Toán học (001)
- BÀI TẬP ĐỊNH LÍ VIÈTE (09)
- BÀI TẬP ĐỊNH LÍ VIÈTE (08)
- BÀI TẬP ĐỊNH LÍ VIÈTE (07)
- Toán thực tế (019)
- BÀI TẬP ĐỊNH LÍ VIÈTE (06)
- BÀI TẬP ĐỊNH LÍ VIÈTE (05)
- BÀI TẬP ĐỊNH LÍ VIÈTE (04)
- BÀI TẬP ĐỊNH LÍ VIÈTE (03)
- BÀI TẬP ĐỊNH LÍ VIÈTE (02)
- BÀI TẬP ĐỊNH LÍ VIÈTE (01)
-
►
May
(17)
Số lượt xem
Hỗ Trợ Trực Tuyến
Vườn Toán - Tin học. Powered by Blogger.