Sunday, February 28, 2016
On 9:59 PM by MATH CHANNEL in Grade 6 Math 1 comment
❄ CONVERTING MANY FRACTIONS TO THE SAME DENOMINATOR
To convert many fractions to the same denominator, we do as follows:
Step 1: Reduce the given fractions, convert their negative denomonators to positive denominators.
Step 2: Find a common denominator (usually LCM)
Step 3: Multiply numerator and denominator of each fraction by corresponding sub-factor (find sub-factor by dividing the common denominator by each denominator)
Step 1: Reduce the given fractions, convert their negative denomonators to positive denominators.
Step 2: Find a common denominator (usually LCM)
Step 3: Multiply numerator and denominator of each fraction by corresponding sub-factor (find sub-factor by dividing the common denominator by each denominator)
Example: Convert the following fractions to the same denominator:
$\dfrac{-4}{{7}}$, $\dfrac{16}{{18}}$ and $\dfrac{20}{{-42}}$
Solution:
$\dfrac{{16}}{{18}} = \dfrac{{8}}{{9}}$, $\dfrac{{20}}{{-42}} = \dfrac{{-10}}{{21}}$
In order to find a common denominator, we often use the following ways:
Way 2: In the three denominators 7, 9, 21, we get the greatest denominator that is 21. We'll multiply 21 by 1, 2, 3, etc until receiving the answer which is divisible by the remaining numbers, that receiving answer is a common denominator. In this case, 21 $\times$ 3 = 63 is divisible by 7, 9, 21. Thus, 21 is common denominator which we have to find.
CD = 63
The 1st sub-factor 63 : 7 = 9, the 2nd sub-factor 63 : 9 = 7, the 3rd sub-factor 63 : 21 = 3
$\dfrac{{ - 4}}{7} = \dfrac{{ - 4 \cdot 9}}{{7 \cdot 9}} = \dfrac{{ - 36}}{{63}}$
$\dfrac{8}{9} = \dfrac{{8 \cdot 7}}{{9 \cdot 7}} = \dfrac{{56}}{{63}}$
$\dfrac{{ - 10}}{{21}} = \dfrac{{ - 10 \cdot 3}}{{21 \cdot 3}} = \dfrac{{ - 30}}{{63}}$
Saturday, February 27, 2016
On 7:11 AM by MATH CHANNEL in Grade 6 Math 1 comment
Rule: In order to reduce a fraction, divide the numerator and denominator by their divisor (other than 1 and $-$1).
$\dfrac{a}{b} = \dfrac{{a : n}}{{b : n}}$ where $n$ $ \in $ CD($a$, $b$)
Note:
_ Fractions in lowest terms (or fractions which can not be reduced further) are fractions such that their numerator and denominator have only 1 and $-$1 as common divisors.
$\dfrac{a}{b} = \dfrac{{a : n}}{{b : n}}$ where $n$ $ \in $ CD($a$, $b$)
Note:
_ Fractions in lowest terms (or fractions which can not be reduced further) are fractions such that their numerator and denominator have only 1 and $-$1 as common divisors.
$\dfrac{a}{b}$ is $a$ fraction in lowest terms $ \Leftrightarrow $ CD($a$, $b$) = $\left\{ { \pm 1} \right\}$
_ When reducing a fraction, we often reduce it to the fraction in lowest terms and has positive denominator.
II. EXAMPLES
Example: Reduce the following fractions:
$\dfrac{{6}}{{8}} = \dfrac{3}{4}$ (divide both the numerator and denominator by 2)
$\dfrac{{ - 5}}{{10}} = \dfrac{{ - 1}}{2}$ (divide both the numerator and denominator by 5)
$\dfrac{{18}}{{ - 33}} = \dfrac{{ - 6}}{{11}}$ (divide both the numerator and denominator by $-$3)
$\dfrac{{ - 36}}{{ - 12}} = \dfrac{3}{1} = 3$ (divide both the numerator and denominator by $-$12)
Friday, February 26, 2016
On 7:34 AM by MATH CHANNEL in Grade 6 Math 1 comment
Fractions are written in the form $\dfrac{a}{b}$ where $a$, $b$ are integers and $b$ is not zero ($a$, $b$ $ \in $ $\mathbb{Z}$, $b \ne 0$), $a$ is the numerator, $b$ is the denominator of the fractions.
Example:
Fractions: $\dfrac{1}{2}$, $\dfrac{-3}{4}$, $\dfrac{7}{-6}$, $\dfrac{-11}{-12}$, etc.
Example:
Fractions: $\dfrac{1}{2}$, $\dfrac{-3}{4}$, $\dfrac{7}{-6}$, $\dfrac{-11}{-12}$, etc.
Not fractions: $\dfrac{1}{0}$, $\dfrac{1.2}{5}$, $ - 9$, etc.
* Comment: Integer $a$ can be written as $\dfrac{a}{1}$.
II. BASIC PROPERTIES OF FRACTIONS
1) $\dfrac{a}{b} = \dfrac{{a \cdot \color{red}m}}{{b \cdot \color{red}m}}$ where $m$ $ \in $ $\mathbb{Z}$ and $m \ne 0$.
2) $\dfrac{a}{b} = \dfrac{{a : \color{red}n}}{{b : \color{red}n}}$ where $n$ $ \in $ CD($a$, $b$).
Tuesday, February 23, 2016
On 8:52 AM by MATH CHANNEL in Grade 6 Math 1 comment
Question: How many zeros are there in the last digits of
the following number:
$P = 11 \times 12 \times \ldots \times 88 \times 89$
(A) 16 (B) 17 (C) 18 (D) 19 (E) None of the above
The number of trailing zeros in the decimal representation of n!, the factorial of a non-negative integer n, is simply the multiplicity of the prime factor 5 in n!. This can be determined with this formula:
$f(n) = \sum\limits_{i = 1}^k {\left\lfloor {\dfrac{n}{{{5^i}}}} \right\rfloor } = \left\lfloor {\dfrac{n}{5}} \right\rfloor + \left\lfloor {\dfrac{n}{{{5^2}}}} \right\rfloor + \left\lfloor {\dfrac{n}{{{5^3}}}} \right\rfloor + \ldots + \left\lfloor {\dfrac{n}{{{5^k}}}} \right\rfloor $, where k must be chosen such that ${5^{k + 1}} > n$
It's more simple if you look at an example:
How many zeros are in the end (after which no other digits follow) of 32! ?
According to above 32! has $\left\lfloor {\dfrac{{32}}{5}} \right\rfloor + \left\lfloor {\dfrac{{32}}{{{5^2}}}} \right\rfloor = 6 + 1 = 7$ (denominator must be less than 32, ${5^2} = 32$ is less)
So, there are 7 zeros in the end of 32!

Monday, February 22, 2016
On 8:35 AM by MATH CHANNEL in Số học 6 2 comments
\[\boxed{\text {Có đúng là: }\dfrac{9}{4} = 2\dfrac{1}{4} = 2{,}25 = 225\% \text { không ?}}\]
I. HỖN SỐ
Ví dụ: $7$ chia cho $4$ được $1$ dư $3$.
Khi đó, ta viết: $\boxed{\dfrac{7}{4} = 1 + \dfrac{3}{4} = 1\dfrac{3}{4}}$. Số $1\dfrac{3}{4}$ là hỗn số, trong đó 1 là phần nguyên, $\dfrac{3}{4}$ là phần phân số của $\dfrac{7}{4}$.
❄ Đổi hỗn số sang phân số:
$5\dfrac{1}{7} = \dfrac{{5 \cdot 7 + 1}}{7} = \dfrac{{36}}{7}$
$\dfrac{7}{3} = 2\dfrac{1}{3}$ ($7$ chia cho $3$ được $2$ dư $1$)
$5\dfrac{1}{7} = \dfrac{{5 \cdot 7 + 1}}{7} = \dfrac{{36}}{7}$
$ - 4\dfrac{3}{5}$ = $\bf-$$\dfrac{{4 \cdot 5 + 3}}{5}$ = $\bf-$$\dfrac{{23}}{5}$
❄ Đổi phân số sang hỗn số:$\dfrac{7}{3} = 2\dfrac{1}{3}$ ($7$ chia cho $3$ được $2$ dư $1$)
$\dfrac{ - 7}{4}$ = $\bf-$$\dfrac{7}{4}$ = $\bf-$$ 1 \dfrac{3}{4}$
II. SỐ THẬP PHÂN
- Phân số thập phân là phân số mà mẫu là lũy thừa của $10$ (Vd: $\dfrac{3}{{10}}$, $\dfrac{{ - 152}}{{100}}$, $\dfrac{{73}}{{1000}}$, ...).
- Phân số thập phân thường viết dưới dạng số thập phân.
- Số thập phân gồm hai phần:
+ Phần số nguyên viết bên trái dấu phẩy,
+ Phần thập phân viết bên phải dấu phẩy.
Ví dụ: $\dfrac{3}{{10}} = \color{black}{0{,}3}$; $\dfrac{-152}{{100}} = \color{black}{-1{,}52}$; $\dfrac{73}{{1000}} = \color{black}{0{,}073}$; ... là các số thập phân.
- Số chữ số của phần thập phân đúng bằng số chữ số $0$ ở mẫu của phân số thập phân.
❄ Đổi phân số thập phân sang số thập phân:
$\dfrac{{27}}{{100}} = 0{,}27$
$\dfrac{{ - 13}}{{1000}} = - 0{,}013$
$\dfrac{{261}}{{100000}} = 0{,}00261$
❄ Đổi số thập phân sang phân số thập phân:
$1{,}21 = \dfrac{{121}}{{100}}$
$0{,}07 = \dfrac{{7}}{{100}}$
$-2{,}013 = \dfrac{{-2013}}{{1000}}$
Những phân số có mẫu là $100$ còn được viết dưới dạng phần trăm với kí hiệu $\%$.
Ví dụ: $\dfrac{3}{{100}} = 3\% $
$\dfrac{107}{{100}} = 107\% $
$\dfrac{7}{{25}} = \dfrac{{28}}{{100}} = 28\% $
$\dfrac{{26}}{{65}} = \dfrac{2}{5} = \dfrac{{40}}{{100}} = 40\% $
$3{,}7 = \dfrac{{37}}{{10}} = \dfrac{{370}}{{100}} = 370\% $
$0{,}34 = \dfrac{{34}}{{100}} = 34\% $
❄ Đổi phần trăm sang số thập phân:
$7\% = 0{,}07$
$45\% = 0{,}45$
$216\% = 2{,}16$
Saturday, February 13, 2016
Bài toán 1: Tìm $n \in $ $\mathbb{N}$ để ba phân số $\dfrac{{21}}{n}$, $\dfrac{{22}}{{n - 1}}$, $\dfrac{{24}}{{n + 1}}$ đều là số tự nhiên.
Bài toán 2: Tìm $n \in $ $\mathbb{Z}$ để $A = \dfrac{{11}}{{n + 1}}$, $B = \dfrac{{6 - 2a}}{{2a + 1}}$ là số nguyên.
Bài toán 3: Chứng tỏ rằng $\dfrac{{21n + 4}}{{14n + 3}}$ là phân số tối giản ($n \in $ $\mathbb{N}$).
Bài toán 4: Tìm tất cả các số tự nhiên $n$ để $\dfrac{{5n + 6}}{{6n + 5}}$ có thể rút gọn được.
Bài toán 5: Với $n \in $ $\mathbb{N}$$^*$, chứng tỏ rằng:
a) $\dfrac{1}{{n(n + 1)}} = \dfrac{1}{n} - \dfrac{1}{{n + 1}}$
b) $\dfrac{2}{{n(n + 1)(n + 2)}} = \dfrac{1}{{n(n + 1)}} - \dfrac{1}{{(n + 1)(n + 2)}}$
Bài toán 6: Chứng tỏ rằng:
a) $\dfrac{1}{{{n^2}}} < \dfrac{1}{{n - 1}} - \dfrac{1}{n}$ ($n \in $ $\mathbb{N}$, $n \ge 2$)
b) $\dfrac{1}{{{n^2}}} > \dfrac{1}{{n}} - \dfrac{1}{n + 1}$ ($n \in $ $\mathbb{N}$, $n \ge 1$)
Bài toán 7: Cho a, b, m $ \in $ $\mathbb{N}$$^*$. Chứng tỏ rằng:
a) $\dfrac{a}{b} > \dfrac{{a + m}}{{b + m}}$ khi $a > b$
b) $\dfrac{a}{b} < \dfrac{{a + m}}{{b + m}}$ khi $a < b$
Bài toán 8: Tính các tổng sau đây:
1) $A = \dfrac{1}{{1 \cdot 2}} + \dfrac{1}{{2 \cdot 3}} + \dfrac{1}{{3 \cdot 4}} + \cdots + \dfrac{1}{{99 \cdot 100}}$
2) $B = \dfrac{5}{{1 \cdot 6}} + \dfrac{5}{{6 \cdot 11}} + \dfrac{5}{{11 \cdot 16}} + \cdots + \dfrac{5}{{96 \cdot 101}}$
3) $C = \dfrac{1}{{1 \cdot 5}} + \dfrac{1}{{5 \cdot 9}} + \dfrac{1}{{9 \cdot 13}} + \cdots + \dfrac{1}{{37 \cdot 41}}$
4) $D = \dfrac{{11}}{{1 \cdot 3}} + \dfrac{{11}}{{3 \cdot 5}} + \dfrac{{11}}{{5 \cdot 7}} + \cdots + \dfrac{{11}}{{97 \cdot 99}}$
5) $E = \dfrac{1}{{6}} + \dfrac{1}{{10}} + \dfrac{1}{{15}} + \dfrac{1}{{21}} + \dfrac{1}{{28}} + \dfrac{1}{{36}} + \dfrac{1}{{45}} + \dfrac{1}{{55}} + \dfrac{1}{{66}} + \dfrac{1}{{78}} + \dfrac{1}{{91}} + \dfrac{1}{{105}}$
6) $F = \dfrac{1}{{1 \cdot 2 \cdot 3}} + \dfrac{1}{{2 \cdot 3 \cdot 4}} + \dfrac{1}{{3 \cdot 4 \cdot 5}} + \cdots + \dfrac{1}{{98 \cdot 99 \cdot 100}}$
7) $G = \dfrac{1}{{2 \cdot 7 \cdot 12}} + \dfrac{1}{{7 \cdot 12 \cdot 17}} + \dfrac{1}{{12 \cdot 17 \cdot 22}} + \cdots + \dfrac{1}{{1997 \cdot 2002 \cdot 2007}}$
8) $H = \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + \ldots + \dfrac{1}{{{2^{2004}}}}$
9) $I = \dfrac{7}{{10}} + \dfrac{7}{{{{10}^2}}} + \dfrac{7}{{{{10}^3}}} + \ldots $
10) $J = 1 + \dfrac{1}{2}\left( {1 + 2} \right) + \dfrac{1}{3}\left( {1 + 2 + 3} \right) + \dfrac{1}{4}\left( {1 + 2 + 3 + 4} \right) + \cdots + $
$ + \dfrac{1}{{16}}\left( {1 + 2 + 3 + \cdots + 16} \right)$
Bài toán 9: Thực hiện phép tính:
2) $- \dfrac{1}{{90}} - \dfrac{1}{{72}} - \dfrac{1}{{56}} - \dfrac{1}{{42}} - \dfrac{1}{{30}} - \dfrac{1}{{20}} - \dfrac{1}{{12}} - \dfrac{1}{6} - \dfrac{1}{2}$
3) $\dfrac{3}{2} - \dfrac{5}{6} + \dfrac{7}{{12}} - \dfrac{9}{{20}} + \dfrac{{11}}{{30}} - \dfrac{{13}}{{42}} + \dfrac{{15}}{{56}} - \dfrac{{17}}{{72}}$
4) $\left( {1 + \dfrac{1}{{1 \cdot 3}}} \right)\left( {1 + \dfrac{1}{{2 \cdot 4}}} \right)\left( {1 + \dfrac{1}{{3 \cdot 5}}} \right) \ldots \left( {1 + \dfrac{1}{{17 \cdot 19}}} \right)\left( {1 + \dfrac{1}{{18 \cdot 20}}} \right)$
5) $\left( {\dfrac{6}{8} + 1} \right)\left( {\dfrac{6}{{18}} + 1} \right)\left( {\dfrac{6}{{30}} + 1} \right) \cdots \left( {\dfrac{6}{{10700}} + 1} \right)$
6) $\left( {1 - \dfrac{1}{3}} \right)\left( {1 - \dfrac{1}{6}} \right)\left( {1 - \dfrac{1}{{10}}} \right)\left( {1 - \dfrac{1}{{15}}} \right) \cdots \left( {1 - \dfrac{1}{{190}}} \right)$
7) $\left( {1 - \dfrac{4}{1}} \right)\left( {1 - \dfrac{4}{9}} \right)\left( {1 - \dfrac{4}{{25}}} \right) \cdots \left( {1 - \dfrac{4}{{38809}}} \right)$
8) $\dfrac{{\left( {1 + 17} \right)\left( {1 + \dfrac{{17}}{2}} \right)\left( {1 + \dfrac{{17}}{3}} \right) \cdots \left( {1 + \dfrac{{17}}{{19}}} \right)}}{{\left( {1 + 19} \right)\left( {1 + \dfrac{{19}}{2}} \right)\left( {1 + \dfrac{{19}}{3}} \right) \cdots \left( {1 + \dfrac{{19}}{{17}}} \right)}}$
4) $\left( {1 + \dfrac{1}{{1 \cdot 3}}} \right)\left( {1 + \dfrac{1}{{2 \cdot 4}}} \right)\left( {1 + \dfrac{1}{{3 \cdot 5}}} \right) \ldots \left( {1 + \dfrac{1}{{17 \cdot 19}}} \right)\left( {1 + \dfrac{1}{{18 \cdot 20}}} \right)$
5) $\left( {\dfrac{6}{8} + 1} \right)\left( {\dfrac{6}{{18}} + 1} \right)\left( {\dfrac{6}{{30}} + 1} \right) \cdots \left( {\dfrac{6}{{10700}} + 1} \right)$
6) $\left( {1 - \dfrac{1}{3}} \right)\left( {1 - \dfrac{1}{6}} \right)\left( {1 - \dfrac{1}{{10}}} \right)\left( {1 - \dfrac{1}{{15}}} \right) \cdots \left( {1 - \dfrac{1}{{190}}} \right)$
7) $\left( {1 - \dfrac{4}{1}} \right)\left( {1 - \dfrac{4}{9}} \right)\left( {1 - \dfrac{4}{{25}}} \right) \cdots \left( {1 - \dfrac{4}{{38809}}} \right)$
8) $\dfrac{{\left( {1 + 17} \right)\left( {1 + \dfrac{{17}}{2}} \right)\left( {1 + \dfrac{{17}}{3}} \right) \cdots \left( {1 + \dfrac{{17}}{{19}}} \right)}}{{\left( {1 + 19} \right)\left( {1 + \dfrac{{19}}{2}} \right)\left( {1 + \dfrac{{19}}{3}} \right) \cdots \left( {1 + \dfrac{{19}}{{17}}} \right)}}$
Bài toán 10: Cho ba số $a$, $b$, $c$ thỏa mãn $abc = 105$ và $bc + b +1$ $ \ne $ 0. Tính giá trị của biểu thức $S = \dfrac{{105}}{{abc + ab + a}} + \dfrac{b}{{bc + b + 1}} + \dfrac{a}{{ab + a + 105}}$.
Bài toán 11: Chứng tỏ rằng:
$\left( {1 + \dfrac{1}{3} + \dfrac{1}{5} + \cdots + \dfrac{1}{{101}}} \right) - \left( {\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6} + \cdots + \dfrac{1}{{100}} + \dfrac{1}{{102}}} \right) = $
$ = \dfrac{1}{{52}} + \dfrac{1}{{53}} + \dfrac{1}{{54}} + \cdots + \dfrac{1}{{101}} + \dfrac{1}{{102}}$
Bài toán 12: Chứng tỏ rằng:
1) $\dfrac{1}{{1 \cdot 2}} + \dfrac{1}{{2 \cdot 3}} + \dfrac{1}{{3 \cdot 4}} + \cdots + \dfrac{1}{{n(n + 1)}} < 1$ ($n \in $ $\mathbb{N}$$^*$)
2) $\dfrac{1}{{{1^2}}} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + \cdots + \dfrac{1}{{{n^2}}} < 2$ ($n \in $ $\mathbb{N}$, $n \ge 2$)
3) $\dfrac{{{{10}^8} + 2}}{{{{10}^8} - 1}} < \dfrac{{{{10}^8}}}{{{{10}^8} - 3}}$
4) $\dfrac{{{{10}^{2004}} + 1}}{{{{10}^{2005}} + 1}} > \dfrac{{{{10}^{2005}} + 1}}{{{{10}^{2006}} + 1}}$
5) $\dfrac{{2000}}{{2001}} + \dfrac{{2001}}{{2002}} > \dfrac{{2000 + 2001}}{{2001 + 2002}}$
6) $\dfrac{1}{{11}} + \dfrac{1}{{12}} + \dfrac{1}{{13}} + \dfrac{1}{{14}} + \dfrac{1}{{15}} + \dfrac{1}{{16}} + \dfrac{1}{{17}} + \dfrac{1}{{18}} + \dfrac{1}{{19}} + \dfrac{1}{{20}} > \dfrac{1}{2}$
7) $\dfrac{1}{5} + \dfrac{1}{{13}} + \dfrac{1}{{14}} + \dfrac{1}{{15}} + \dfrac{1}{{61}} + \dfrac{1}{{62}} + \dfrac{1}{{63}} < \dfrac{1}{2}$
8) $\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \cdots + \dfrac{1}{{63}} > 2$
8) $\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \cdots + \dfrac{1}{{63}} > 2$
Bài toán 13: Cho a, b, c, d > 0. Chứng tỏ rằng:
a) $\dfrac{{a + b}}{{1 + a + b}} \le \dfrac{a}{{1 + a}} + \dfrac{b}{{1 + b}}$
b) $1 < \dfrac{a}{{a + b + c}} + \dfrac{b}{{b + c + d}} + \dfrac{c}{{c + d + a}} + \dfrac{d}{{d + a + b}} < 2$
Bài toán 14: Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó thì không nhỏ hơn 2.
Wednesday, February 10, 2016
I. PHÉP CỘNG PHÂN SỐ
❄ Cộng hai phân số cùng mẫu: $\boxed{\dfrac{a}{m} + \dfrac{b}{m} = \dfrac{{a + b}}{m}}$
❄ Cộng hai phân số không cùng mẫu: Ta qui đồng các phân số rồi áp dụng công thức trên.
Ví dụ: Tính:
1) $\dfrac{3}{8} + \dfrac{5}{8} = \dfrac{{3 + 5}}{8} = \dfrac{8}{8} = 1$
2) $\dfrac{1}{7} + \dfrac{{ - 4}}{7} = \dfrac{{1 + ( - 4)}}{7} = \dfrac{{ - 3}}{7}$
3) $\dfrac{6}{{18}} + \dfrac{{ - 14}}{{21}} = \dfrac{1}{3} + \dfrac{{ - 2}}{3} = \dfrac{{1 + ( - 2)}}{3} = \dfrac{{ - 1}}{3}$
4) $\dfrac{{ - 2}}{3} + \dfrac{4}{{15}} = \dfrac{{ - 10}}{{15}} + \dfrac{4}{{15}} = \dfrac{{ - 6}}{{15}} = \dfrac{{ - 2}}{5}$
5) $\dfrac{{11}}{{15}} + \dfrac{9}{{ - 10}} = \dfrac{{11}}{{15}} + \dfrac{{ - 9}}{{10}} = \dfrac{{22}}{{30}} + \dfrac{{ - 27}}{{30}} = \dfrac{{ - 5}}{{30}} = \dfrac{{ - 1}}{6}$
6) $\dfrac{1}{{ - 7}} + 3 = \dfrac{{ - 1}}{7} + \dfrac{3}{1} = \dfrac{{ - 1}}{7} + \dfrac{{21}}{7} = \dfrac{{20}}{7}$
Tương tự phép cộng số nguyên, phép cộng phân số có các tính chất cơ bản sau:
a) Giao hoán: $\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{c}{d} + \dfrac{a}{b}$
b) Kết hợp: $\left( {\dfrac{a}{b} + \dfrac{c}{d}} \right) + \dfrac{p}{q} = \dfrac{a}{b} + \left( {\dfrac{c}{d} + \dfrac{p}{q}} \right)$
c) Cộng với số $0$: $\dfrac{a}{b} + 0 = 0 + \dfrac{a}{b} = \dfrac{a}{b}$
❄ Cộng hai phân số không cùng mẫu: Ta qui đồng các phân số rồi áp dụng công thức trên.
Ví dụ: Tính:
1) $\dfrac{3}{8} + \dfrac{5}{8} = \dfrac{{3 + 5}}{8} = \dfrac{8}{8} = 1$
2) $\dfrac{1}{7} + \dfrac{{ - 4}}{7} = \dfrac{{1 + ( - 4)}}{7} = \dfrac{{ - 3}}{7}$
3) $\dfrac{6}{{18}} + \dfrac{{ - 14}}{{21}} = \dfrac{1}{3} + \dfrac{{ - 2}}{3} = \dfrac{{1 + ( - 2)}}{3} = \dfrac{{ - 1}}{3}$
4) $\dfrac{{ - 2}}{3} + \dfrac{4}{{15}} = \dfrac{{ - 10}}{{15}} + \dfrac{4}{{15}} = \dfrac{{ - 6}}{{15}} = \dfrac{{ - 2}}{5}$
5) $\dfrac{{11}}{{15}} + \dfrac{9}{{ - 10}} = \dfrac{{11}}{{15}} + \dfrac{{ - 9}}{{10}} = \dfrac{{22}}{{30}} + \dfrac{{ - 27}}{{30}} = \dfrac{{ - 5}}{{30}} = \dfrac{{ - 1}}{6}$
6) $\dfrac{1}{{ - 7}} + 3 = \dfrac{{ - 1}}{7} + \dfrac{3}{1} = \dfrac{{ - 1}}{7} + \dfrac{{21}}{7} = \dfrac{{20}}{7}$
Tương tự phép cộng số nguyên, phép cộng phân số có các tính chất cơ bản sau:
a) Giao hoán: $\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{c}{d} + \dfrac{a}{b}$
b) Kết hợp: $\left( {\dfrac{a}{b} + \dfrac{c}{d}} \right) + \dfrac{p}{q} = \dfrac{a}{b} + \left( {\dfrac{c}{d} + \dfrac{p}{q}} \right)$
c) Cộng với số $0$: $\dfrac{a}{b} + 0 = 0 + \dfrac{a}{b} = \dfrac{a}{b}$
II. PHÉP TRỪ PHÂN SỐ
Qui tắc: $\boxed{{\dfrac{a}{b} \color{red}{-} \dfrac{c}{d} = \dfrac{a}{b} + \dfrac{{ \color{red}{-} c}}{d}}}$
Mẹo: Để thực hiện phép trừ, ta đem dấu "$-$" (màu đỏ) lên tử của phân số thứ hai và thay chỗ trống đó bằng dấu "$+$".
Lưu ý: $\boxed{\dfrac{a}{{ - b}} = - \dfrac{a}{b} = \dfrac{{ - a}}{b}}$
Ví dụ: Tính:1) $\dfrac{1}{8} - \dfrac{1}{2} = \dfrac{1}{8} + \dfrac{{ - 1}}{2} = \dfrac{1}{8} + \dfrac{{ - 4}}{8} = \dfrac{{ - 3}}{8}$
2) $\dfrac{{ - 5}}{7} - \dfrac{1}{3} = \dfrac{{ - 5}}{7} + \dfrac{{ - 1}}{3} = \dfrac{{ - 15}}{{21}} + \dfrac{{ - 7}}{{21}} = \dfrac{{ - 22}}{{21}}$
3) $\dfrac{3}{5} - \dfrac{{ - 1}}{2} = \dfrac{3}{5} + \dfrac{1}{2} = \dfrac{6}{{10}} + \dfrac{5}{{10}} = \dfrac{{11}}{{10}}$
4) $\dfrac{{ - 2}}{5} - \dfrac{{ - 3}}{4} = \dfrac{{ - 2}}{5} + \dfrac{3}{4} = \dfrac{{ - 8}}{{20}} + \dfrac{{15}}{{20}} = \dfrac{7}{{20}}$
5) $ - 5 - \dfrac{1}{6} = \dfrac{{ - 5}}{1} + \dfrac{{ - 1}}{6} = \dfrac{{ - 30}}{6} + \dfrac{{ - 1}}{6} = \dfrac{{ - 31}}{6}$
III. PHÉP NHÂN PHÂN SỐ
Qui tắc: $\boxed{\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{{a \cdot c}}{b \cdot d}}$
Ví dụ: Tính:
1) $\dfrac{{ - 3}}{7} \cdot \dfrac{2}{{ - 5}} = \dfrac{{( - 3) \cdot 2}}{{7 \cdot ( - 5)}} = \dfrac{{ - 6}}{{ - 35}} = \dfrac{6}{{35}}$
2) $\dfrac{{ - 28}}{{33}} \cdot \dfrac{{ - 3}}{4} = \dfrac{{( - 28) \cdot ( - 3)}}{{33 \cdot 4}} = \dfrac{{\color{red}{28} \cdot \color{blue}{3}}}{{\color{blue}{33} \cdot \color{red}{4}}} = \dfrac{{\color{red}{7} \cdot \color{blue}{1}}}{{\color{blue}{11} \cdot \color{red}{1}}} = \dfrac{7}{{11}}$
3) ${\left( {\dfrac{{ - 3}}{5}} \right)^2} = \dfrac{{ - 3}}{5} \cdot \dfrac{{ - 3}}{5} = \dfrac{9}{{25}}$
4) ${\left( { - \dfrac{3}{2}} \right)^5} = \left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right)\left( { - \dfrac{3}{2}} \right) = - \dfrac{{{3^5}}}{{{2^5}}} = - \dfrac{{243}}{{32}}$
5) $( - 2) \cdot \dfrac{{ - 3}}{7} = \dfrac{{( - 2) \cdot ( - 3)}}{7} = \dfrac{6}{7}$ $\left(a \cdot \dfrac{b}{c} \color{orange}{ = \dfrac{a}{1} \cdot \dfrac{b}{c}} = \dfrac{{a \cdot b}}{c}\right)$
6) $\dfrac{5}{{33}} \cdot (-3) = \dfrac{{5 \cdot \color{red}{( - 3)}}}{\color{red}{33}} = \dfrac{{5 \cdot \color{red}{( - 1)}}}{\color{red}{11}} = \dfrac{{ - 5}}{{11}}$ $\left(\dfrac{a}{b} \cdot c \color{orange}{ = \dfrac{a}{b} \cdot \dfrac{c}{1}} = \dfrac{{a \cdot c}}{b}\right)$
Tương tự phép nhân số nguyên, phép nhân phân số có các tính chất cơ bản sau:
a) Giao hoán: $\dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{c}{d} \cdot \dfrac{a}{b}$
b) Kết hợp: $\left( {\dfrac{a}{b} \cdot \dfrac{c}{d}} \right) \cdot \dfrac{p}{q} = \dfrac{a}{b} \cdot \left( {\dfrac{c}{d} \cdot \dfrac{p}{q}} \right)$
c) Nhân với số 1: $\dfrac{a}{b} \cdot 1 = 1 \cdot \dfrac{a}{b} = \dfrac{a}{b}$
d) Phân phối: $\dfrac{a}{b} \cdot \left( {\dfrac{c}{d} \pm \dfrac{p}{q}} \right) = \dfrac{a}{b} \cdot \dfrac{c}{d} \pm \dfrac{a}{b} \cdot \dfrac{p}{q}$
IV. PHÉP CHIA PHÂN SỐ
Qui tắc: $\boxed{\dfrac{a}{b}:\dfrac{c}{d} = \dfrac{a}{b} \cdot \dfrac{d}{c} = \dfrac{{a \cdot d}}{{b \cdot c}}\;\left( {c \ne 0} \right)}$
Ví dụ: Tính:
1) $\dfrac{5}{6}:\dfrac{{ - 7}}{{12}} = \dfrac{5}{6} \cdot \dfrac{{ - 12}}{7} = \dfrac{5}{1} \cdot \dfrac{{ - 2}}{7} = \dfrac{{ - 10}}{7}$
2) $ - 7:\dfrac{{14}}{3} = - 7 \cdot \dfrac{3}{{14}} = \dfrac{{ - 3}}{2}$
3) $\dfrac{{ - 3}}{7}:9 = \dfrac{{ - 3}}{7} \cdot \dfrac{1}{9} = \dfrac{{ - 1}}{7} \cdot \dfrac{1}{3} = \dfrac{{ - 1}}{{21}}$
Sunday, February 7, 2016
On 8:57 AM by MATH CHANNEL in Toán và cuộc sống 1 comment
Các bạn hãy cùng chiêm ngưỡng vẻ đẹp của số 2016 nhé!
$2016 = {11111100000_2}$
$2016 = {2^{11}} - {2^5}$
$2016 = {2^{6 - 1}} \times \left( {{2^6} - 1} \right)$
$2016 = 2 \times 7! \div 5$
$2016 = {2^5} \times {3^2} \times 7$
$2016 = 1 + 2 + 3 + \ldots + 63 = \sum\limits_{k = 1}^{63} k $
$2016 = 1 + 5 + 9 + 13 + \ldots + 125 = \sum\limits_{k = 0}^{31} {(4k + 1)} $
$2016 = {2^{10}} + {2^9} + {2^8} + {2^7} + {2^6} + {2^5}$
$2016 = {3^3} + {4^3} + {5^3} + {6^3} + {7^3} + {8^3} + {9^3}$
$2016 = {2^3} + {4^3} + {6^3} + {12^3}$
$2016 = 2 \times \left( {{3^2} + {3^3} + {3^{2 + 3}} + {3^{2 \times 3}}} \right)$
$2016 = {1^2} - {2^2} + {3^2} - {4^2} + \ldots - {62^2} + {63^2} = \sum\limits_{k = 1}^{63} {{{( - 1)}^{k + 1}}{k^2}} $
$2016 = \sqrt {{1^3} + {2^3} + {3^3} + \ldots + {{62}^3} + {{63}^3}} = \sqrt {\sum\limits_{k = 1}^{63} {{k^3}} } $
$2016 = {11^4} - {10^4} - {9^4} + {8^4} - {7^4} + {6^4} + {5^4} + {4^4} + {3^4} - {2^4} - {1^4}$
$2016 = 9!! + 8!! + 7!! + 6! - 5! - 4! + 3! - 2! + 1! + 0!$
$2016 = 1 + 2 + 4 + 8 + 16 + 32 + 63 + 126 + 252 + 504 + 1008$
$2016 = 666 + 666 + 666 + 6 + 6 + 6$
$2016 = 888 + 888 + 88 + 88 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8$
$2016 = 999 + 999 + 9 + 9$
$2016 = 888 + 666 + 444 + 8 + 6 + 4$
$2016 = 999 + 777 + 99 + 77 + 9 + 7 + 9 + 7 + 9 + 7 + 9 + 7$
$2016 = 1234 + 567 + 89 + 123 + 1 + 2$
$2016 = 1243 + 5 + 678 + 90$
$2016 = 987 + 654 + 321 + 9 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1$
Friday, February 5, 2016
On 9:21 PM by MATH CHANNEL in Số học 6 2 comments
❄ SO SÁNH HAI PHÂN SỐ
Để so sánh hai phân số ta thường sử dụng hai cách sau:
Cách 1: Qui đồng mẫu (xem tại đây) hoặc tử.
Cách 2: Thông qua giá trị trung gian (số nguyên hoặc phân số).Lưu ý:
1) Phân số có tử và mẫu cùng dấu thì lớn hơn 0, phân số lớn hơn 0 gọi là phân số dương. Ngược lại, phân số có tử và mẫu khác dấu thì nhỏ hơn 0, phân số nhỏ hơn 0 gọi là phân số âm.
2) Với phân số dương (tử và mẫu cùng dấu), nếu tử lớn hơn mẫu thì phân số lớn hơn 1 và ngược lại.
3) Với hai phân số dương cùng tử, phân số nào có mẫu nhỏ hơn thì lớn hơn và ngược lại.
4) Cho hai phân số $\dfrac{a}{b}$ và $\dfrac{c}{d}$ ($a$, $b$, $c$, $d$ $\in$ $\mathbb{N}^*$, $a$ < $c$, $b$ > $d$) thì $\dfrac{a}{b} < \dfrac{c}{b} < \dfrac{c}{d}$
5) Nếu chỉ so sánh hai phân số có bằng nhau hay không ta sử dụng tính chất $\dfrac{a}{b} = \dfrac{c}{d} \Leftrightarrow a \cdot d = b \cdot c$
Ví dụ 1: Các cặp phân số sau có bằng nhau hay không?
1) $\dfrac{2}{3}$ và $\dfrac{6}{9}$
$\dfrac{2}{3} = \dfrac{6}{9}$ vì $2 \cdot 9 = 3 \cdot 6$.
2) $\dfrac{{ - 3}}{4}$ và $\dfrac{5}{{ - 7}}$
$\dfrac{{ - 3}}{4} \ne \dfrac{5}{{ - 7}}$ vì $( - 3) \cdot ( - 7) \ne 4 \cdot 5$.
Ví dụ 2: So sánh các phân số
1) $\dfrac{14}{{21}}$ và $\dfrac{ - 60}{{ - 72}}$
$\dfrac{{14}}{{21}} = \dfrac{{2}}{{3}}$, $\dfrac{{ - 60}}{{ - 72}} = \dfrac{{5}}{{6}}$
MC = 6
$\dfrac{2}{3} = \dfrac{{2 \cdot 2}}{{3 \cdot 2}} = \dfrac{4}{6}$
Vì $\dfrac{{4}}{{6}} < \dfrac{{ 5}}{6}$
nên $\dfrac{{14}}{{21}} < \dfrac{{ - 60}}{ - 72}$.
2) $\dfrac{-2}{{7}}$ và $\dfrac{24}{{-56}}$
$\dfrac{{24}}{{ - 56}} = \dfrac{{ - 3}}{{7}}$ (chia cả tử và mẫu cho $-8$)
Vì $\dfrac{{-2}}{{7}} > \dfrac{{ - 3}}{7}$
nên $\dfrac{{-2}}{{7}} > \dfrac{{24}}{-56}$.
3) $\dfrac{11033}{{15045}}$ và $\dfrac{1111}{{1515}}$
$\dfrac{{11033}}{{15045}} = \dfrac{{11}}{{15}}$ (chia cả tử và mẫu cho $1003$)
$\dfrac{{1111}}{{1515}} = \dfrac{{11}}{{15}}$ (chia cả tử và mẫu cho $101$)
Vậy $\dfrac{{11033}}{{15045}} = \dfrac{{1111}}{{1515}}$.
4) $\dfrac{141}{{893}}$ và $\dfrac{159}{{901}}$
$\dfrac{{141}}{{893}} = \dfrac{3}{{19}}$, $\dfrac{{159}}{{901}} = \dfrac{3}{{17}}$
Vì $\dfrac{{3}}{{19}} < \dfrac{{3}}{17}$
nên $\dfrac{{141}}{{893}} < \dfrac{{159}}{901}$.
5) $\dfrac{ - 19}{{7}}$ và $\dfrac{1}{{6}}$
$\dfrac{{ - 19}}{7} < 0 < \dfrac{1}{6}$
$ \Rightarrow $ $\dfrac{{ - 19}}{7} < \dfrac{1}{6}$.
6) $\dfrac{{79}}{{97}}$ và $\dfrac{71}{{17}}$
$\dfrac{{79}}{97} < 1 < \dfrac{71}{17}$
$ \Rightarrow $ $\dfrac{{79}}{97} < \dfrac{71}{17}$.
7) $\dfrac{{37}}{{195}}$ và $\dfrac{73}{{179}}$
$\dfrac{{37}}{{195}} < \dfrac{{73}}{{195}} < \dfrac{{73}}{{179}}$
$ \Rightarrow $ $\dfrac{{37}}{{195}} < \dfrac{{73}}{{179}}$.
8) $\dfrac{{12}}{{29}}$ và $\dfrac{16}{{41}}$
$\dfrac{{12}}{{29}} > \dfrac{{12}}{{30}} = \dfrac{2}{5} = \dfrac{{16}}{{40}} > \dfrac{{16}}{{41}}$
$ \Rightarrow $ $\dfrac{{12}}{{29}} > \dfrac{{16}}{{41}}$.
9) $\dfrac{{22}}{{7}}$ và $\dfrac{34}{{11}}$
$\dfrac{{22}}{7} = 3\dfrac{1}{7}\;\left( { = 3 + \dfrac{1}{7}} \right)$, $\dfrac{{34}}{{11}} = 3\dfrac{1}{{11}}\;\left( { = 3 + \dfrac{1}{{11}}} \right)$
Vì $\dfrac{{1}}{{7}} > \dfrac{{1}}{11}$
nên $\dfrac{{22}}{{7}} > \dfrac{{34}}{11}$.
Subscribe to:
Comments (Atom)
Search
Popular Posts
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Hình thang cân 1. Hình thang có hai góc kề một đáy bằng nhau là hìn...
-
$\boxed{\text {Bổ đề hình thang: }}$ Trong hình thang hai đáy không bằng nhau, giao điểm của hai đường thẳng chứa hai cạnh bên, giao điể...
-
SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TAM GIÁC DẤU HIỆU NHẬN BIẾT CÁC HÌNH Tam giác cân 1. Tam giác có hai cạnh bằng nhau là tam giác cân....
-
$\boxed{\text {Bài toán: }}$ Cho O, H, G lần lượt là tâm đường tròn ngoại tiếp, trực tâm, trọng tâm của $\triangle$ ABC. Chứng minh rằng...
-
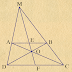
$\boxed{\text {Bài toán 1: }}$ (Đề thi HKII 2008-2009 Q11 TpHCM) Cho tam giác ABC có các góc đều nhọn và có ba đường cao là AD, BE, CF c...
-
Để tìm ƯCLN, BCNN của các số tự nhiên, người ta thường dùng những cách sau: Cách 1 : Phân tích các số ra thừa số nguyên tố Vd: Tìm ƯC...
-
Bạn cần download tài liệu, ebook,... phục vụ cho việc học tập nghiên cứu từ các trang Scribd, Issuu, Slideshare và Academia một cách nhanh...
-
Chương trình Tìm Ước chung lớn nhất và Bội chung nhỏ nhất của một dãy các số tự nhiên import java.util.Scanner; public class Main ...
-
Dãy số Fibonacci được định nghĩa như sau: F[0] =1, F[1] = 1; F[n] = F[n-1] + F[n-2] với n>=2. Hãy viết chương trình tìm số Fibonacci thứ ...
-
Chương trình Chuyển đổi một số tự nhiên ở hệ thập phân thành số ở hệ nhị phân, bát phân, thập lục phân và hệ cơ số bất kì import java.u...
Recent Posts
Categories
- Công nghệ thông tin
- Đại số 10
- Đại số 7
- Đại số 8
- Đại số 9
- Đề thi Toán 6
- Đề thi Toán 7
- Đề thi Toán 8
- Đề thi Toán 9
- Đố Toán
- Grade 6 Math
- Grade 8 Math
- Grade 9 Math
- Hình học 6
- Hình học 7
- Hình học 8
- Hình học 9
- Khác
- Lập trình Java cơ bản
- Math Puzzles
- Mathematical game
- Phương pháp học Toán
- Số học 6
- Số và Đại số 6
- Toán tham khảo 6
- Toán tham khảo 8
- Toán tham khảo 9
- Toán thực tế
- Toán và cuộc sống
Blog Archive
-
▼
2016
(91)
-
▼
February
(12)
- [Arithmetic 6] Converting many fractions to the sa...
- [Arithmetic 6] Reducing a fraction
- [Arithmetic 6] Extending the concept of fractions
- [Arithmetic 6] Advanced exercises
- [SỐ HỌC 6] HỖN SỐ - SỐ THẬP PHÂN - PHẦN TRĂM
- [SỐ HỌC 6] TOÁN NÂNG CAO VỀ PHÂN SỐ
- [SỐ HỌC 6] CÁC PHÉP TOÁN TRONG PHÂN SỐ
- Số 2016 trong Toán học
- [SỐ HỌC 6] SO SÁNH PHÂN SỐ
- [SỐ HỌC 6] QUI ĐỒNG MẪU CÁC PHÂN SỐ
- [ĐẠI SỐ 9] CÁC PHÉP BIẾN ĐỔI BIỂU THỨC CHỨA CĂN
- [HÌNH HỌC 6] THỰC HÀNH ĐO GÓC
-
▼
February
(12)
Số lượt xem
Hỗ Trợ Trực Tuyến
Vườn Toán - Tin học. Powered by Blogger.